容量制約ありVRPのためのMIPソルバー定式化の性能比較

容量制約ありVRPのためのMIPソルバー定式化の性能比較#

ここでは、Capacitated Vehicle Routing Problem (CVRP)の異なる定式化を、MIPソルバーを用いて解いたときの性能から比較してみましょう。 CVRPはVRPの一種です。 各顧客には需要があり、車両には容量の制約があります。 CVRPはVRPを一般化したものであり、CVRPの特殊ケースと見なすことができます。
各モデルをJijModelingを用いて実装し、最適化結果をMINTOで管理、そしてSCIPによりモデルを解いてみましょう。 最後に、各モデルのパフォーマンスを比較します。

MTZ定式化とフロー定式化#

CVRPには主に、MTZ定式化 (ポテンシャル定式化とも呼ばれる) とフロー定式化という2つの定式化があります。

各定式化について#

MTZ定式化とフロー定式化では、累積需要の追跡の仕方が異なります。 MTZ定式化は各顧客ノードにおける累積需要を追跡するのに対し、フロー定式化は各エッジにおけるフロー量を追跡します。

  • MTZ (Miller-Tucker-Zemlin) 定式化: MTZ定式化では、各顧客ノードにおける累積需要を表す連続変数を導入し、部分順回路除去制約を表現します。この方法は変数の総数が比較的少なくて済み、モデルも単純です。しかしLP緩和は弱くなります。

  • フロー定式化: フロー定式化では、各エッジのフロー量を表す連続変数を導入し、フロー保存則を用いて部分巡回路除去制約を表現します。この手法は変数の総数が多くなりますが、LP緩和効果がよりMTZ定式化より極力となります。

それでは、この2つの定式化を実装し、それらの性能を比較してみましょう。

CVRP定式化の共通部分の実装#

まずは、両方のモデルに共通する部分を実装しましょう。

import minto
import jijmodeling as jm
from minto.problems.cvrp import CVRPMTZ, CVRPFlow

MTZ 定式化#

CVRPMTZ().problem()
\[\begin{split}\begin{array}{cccc}\text{Problem:} & \text{CVRPMTZ} & & \\& & \min \quad \displaystyle \sum_{i = 0}^{n - 1} \sum_{j = 0}^{n - 1} c_{i, j} \cdot x_{i, j} & \\\text{{s.t.}} & & & \\ & \text{in} & \displaystyle \sum_{\ast_{1} = 0}^{n - 1} x_{i, \ast_{1}} = 1 & \forall i \in \left\{i \in \left\{0,\ldots,n - 1\right\} \mid i > 0 \right\} \\ & \text{no loop} & \displaystyle x_{i, i} = 0 & \forall i \in \left\{0,\ldots,n - 1\right\} \\ & \text{out} & \displaystyle \sum_{\ast_{0} = 0}^{n - 1} x_{\ast_{0}, i} = 1 & \forall i \in \left\{i \in \left\{0,\ldots,n - 1\right\} \mid i > 0 \right\} \\ & \text{potiantial} & \displaystyle u_{i} + D_{j} - Q \cdot \left(- x_{i, j} + 1\right) + \left(Q - D_{i} - D_{j}\right) \cdot x_{j, i} \leq u_{j} & \forall i \in \left\{0,\ldots,n - 1\right\} \forall j \in \left\{j \in \left\{0,\ldots,n - 1\right\} \mid j \neq 0 \right\} \\\text{{where}} & & & \\& x & 2\text{-dim binary variable}& \text{use edge or not}\\& u & 1\text{-dim continuous variable}& \text{cumulative demand}\\ & & \text{lower bound: }D & \\ & & \text{upper bound: }Q & \\\end{array}\end{split}\]

フロー定式化#

CVRPFlow().problem()
\[\begin{split}\begin{array}{cccc}\text{Problem:} & \text{CVRPFlow} & & \\& & \min \quad \displaystyle \sum_{i = 0}^{n - 1} \sum_{j = 0}^{n - 1} c_{i, j} \cdot x_{i, j} & \\\text{{s.t.}} & & & \\ & \text{flow} & \displaystyle \sum_{j = 0}^{n - 1} f_{j, i} - \sum_{j = 0}^{n - 1} f_{i, j} = D_{i} & \forall i \in \left\{i \in \left\{0,\ldots,n - 1\right\} \mid i > 0 \right\} \\ & \text{flow cap} & \displaystyle f_{i, j} \leq \left(Q - D_{i}\right) \cdot x_{i, j} & \forall i \in \left\{0,\ldots,n - 1\right\} \forall j \in \left\{0,\ldots,n - 1\right\} \\ & \text{in} & \displaystyle \sum_{\ast_{1} = 0}^{n - 1} x_{i, \ast_{1}} = 1 & \forall i \in \left\{i \in \left\{0,\ldots,n - 1\right\} \mid i > 0 \right\} \\ & \text{no loop} & \displaystyle x_{i, i} = 0 & \forall i \in \left\{0,\ldots,n - 1\right\} \\ & \text{out} & \displaystyle \sum_{\ast_{0} = 0}^{n - 1} x_{\ast_{0}, i} = 1 & \forall i \in \left\{i \in \left\{0,\ldots,n - 1\right\} \mid i > 0 \right\} \\\text{{where}} & & & \\& x & 2\text{-dim binary variable}& \text{use edge or not}\\& f & 2\text{-dim continuous variable}& \text{cumulative demand}\\ & & \text{lower bound: }0 & \\ & & \text{upper bound: }Q & \\\end{array}\end{split}\]

ランダムなCVRPインスタンスの生成#

モデルのテストを行うために、ランダムなCVRPインスタンスを生成しましょう。

n = 10
instance_data = CVRPFlow().random_data(n)
xy = instance_data["xy"]

パフォーマンス比較#

先程作成したランダムCVRPインスタンスを用いて、2つの定式化のパフォーマンスを比較しましょう。 JijModelingを用いた実装をommx_pyscipopt_adapterを用いてPySCIPOptに変換し、SCIPを用いて解きます。 結果はMINTOを用いてロギングします。 .log_instanceを用いてログに記録する際、後から比較しやすいように各モデルに名前をつけておきましょう。 このチュートリアルではauto_saving=Falseを設定していますが、実際には自動ログ保存のためにauto_saving=Trueを使用することを推奨します。

import time
import ommx_pyscipopt_adapter as scip_ad

exp = minto.Experiment("cvrp", auto_saving=False, verbose_logging=False)

nlist = [8, 9, 10, 11, 12, 13]
for n in nlist:
    print(f"{n=}")
    with exp.run() as run:
        instance_data = CVRPFlow().random_data(n)
        run.log_parameter("n", n)
        intepreter = jm.Interpreter(instance_data)

        # MTZ model
        mtz_instance = intepreter.eval_problem(CVRPMTZ().problem())
        run.log_instance("mtz", mtz_instance)

        adapter = scip_ad.OMMXPySCIPOptAdapter(mtz_instance)
        scip_model = adapter.solver_input

        start = time.time()
        scip_model.optimize()
        scip_model.getStatus()
        elpsed_time = time.time() - start

        run.log_parameter("mtz_time", elpsed_time)

        mtz_solution = adapter.decode(scip_model)
        run.log_solution("mtz", mtz_solution)

        # Flow model
        intepreter = jm.Interpreter(instance_data)
        flow_instance = intepreter.eval_problem(CVRPFlow().problem())
        run.log_instance("flow", flow_instance)

        adapter = scip_ad.OMMXPySCIPOptAdapter(flow_instance)
        scip_model = adapter.solver_input

        start = time.time()
        scip_model.optimize()
        scip_model.getStatus()
        elpsed_time = time.time() - start

        run.log_parameter("flow_time", elpsed_time)

        flow_solution = adapter.decode(scip_model)
        run.log_solution("flow", flow_solution)

n=8
n=9
n=10
n=11
n=12
n=13

exp.get_run_table()
instance_mtz instance_flow ... solution_flow parameter metadata
num_vars num_binary num_integer num_continuous num_cons title name num_vars num_binary num_integer ... feasible optimality relaxation start name n mtz_time flow_time run_id elapsed_time
run_id
0 90 81 0 9 None None mtz 162 81 0 ... True 1 0 None flow 8 0.373916 1.506538 0 4.268777
1 110 100 0 10 None None mtz 200 100 0 ... True 1 0 None flow 9 1.367615 1.672106 1 5.526553
2 132 121 0 11 None None mtz 242 121 0 ... True 1 0 None flow 10 0.983179 2.807852 2 6.325906
3 156 144 0 12 None None mtz 288 144 0 ... True 1 0 None flow 11 1.999751 1.039342 3 5.444446
4 182 169 0 13 None None mtz 338 169 0 ... True 1 0 None flow 12 67.148398 14.981206 4 84.476499
5 210 196 0 14 None None mtz 392 196 0 ... True 1 0 None flow 13 28.875992 5.319174 5 36.485040

6 rows × 31 columns

import matplotlib.pyplot as plt

param_table = exp.get_run_table()["parameter"]
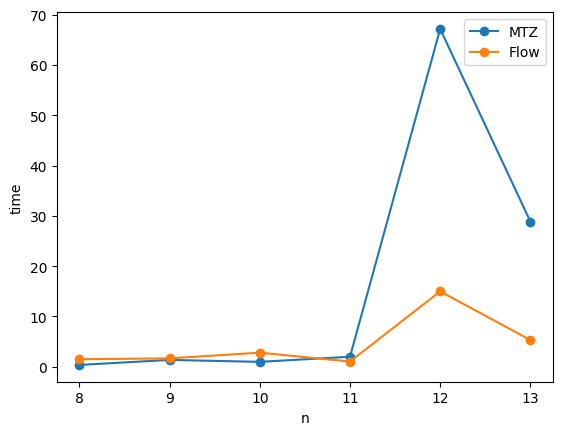
plt.plot(param_table["n"], param_table["mtz_time"], "-o", label="MTZ")
plt.plot(param_table["n"], param_table["flow_time"], "-o", label="Flow")
plt.legend()
plt.xlabel("n")
plt.ylabel("time")
plt.show()
../_images/8609be2a327efb16f1135e73999bfcf8f9bc20acbe2afb5ec3fdd7830767b1fa.png

まとめ#

ここでは、容量制約あり配送計画問題(CVRP)に対するMTZ定式化とフロー定式化を実装し、ランダムなCVRPインスタンスを用いてそれらの性能を比較しました。 与えられたインスタンスでは、フロー定式化の方がMTZ定式化よりも高速であることがわかりました。
変数が多いにも関わらず、フロー定式化の方が性能が優れていたのは興味深い点です。 これは分岐限定法の有効性が、制約条件や解が容易に得られるかどうかに依存してどう変化するかを示す良い例となっています。 しかし、性能はインスタンス特性により変化する可能性もあります。 例えば、車両の容量が異なると、結果が大きく異なる可能性もあります。 さらに、MTZ定式化の強化版も利用可能です。
様々なインスタンス生成方法や強化版のMTZ定式化も、試してみると良いでしょう。

目次