OpenJij SA Parameter Dependency Experiment with MINTO#
This notebook is a simple experiment to see how the parameters of the Simulated Annealing (SA) algorithm in OpenJij affect the performance of the algorithm.
The SA algorithm has temperature as a parameter, and OpenJij automatically sets this temperature based on the coefficients of QUBO or Ising models. Let’s verify how effective these automatic parameter settings are by using grid search.
Even in grid search cases, using MINTO for logging allows us to easily convert the data to pandas.DataFrame for visualization. This helps us analyze the relationship between different parameter combinations and their impact on solution quality and execution time.
import openjij as oj
import numpy as np
import minto
import matplotlib.pyplot as plt
import seaborn as sns
1. Create Random QUBO#
def random_qubo(n, sparsity=0.5):
q = np.random.uniform(-1, 1, (n, n))
q = (q + q.T) / 2
zero_num = int(n**2 * sparsity)
zero_i = np.random.choice(n, zero_num, replace=True)
zero_j = np.random.choice(n, zero_num, replace=True)
q[zero_i, zero_j] = 0
q[zero_j, zero_i] = 0
qubo = {}
for i in range(n-1):
for j in range(i, n):
qubo[(i, j)] = q[i, j]
qubo[(j, i)] = q[j, i]
return qubo
n = 200
q = random_qubo(n)
2. Run with default parameters#
In OpenJij, you can check the automatically configured SA parameters through .info['schedule'] in the return value of .sample_qubo. These parameters are stored under the key ‘schedule’ since the temperature settings in SA are referred to as the annealing schedule.
sampler = oj.SASampler()
response = sampler.sample_qubo(q)
schedule = response.info['schedule']
schedule
{'beta_max': 146262.07805091763,
'beta_min': 0.03395211324880749,
'num_sweeps': 1000}
3. Grid search with MINTO#
Let’s see how the optimization results change by varying the inverse temperature parameters of SA. We’ll include OpenJij’s default parameters in our search range for comparison.
The important values from OpenJij’s results are stored using .log_parameter method. The complete OpenJij response object is also saved using .log_object method with .to_serializable.
exp = minto.Experiment(auto_saving=False)
# log_object accepts only serializable objects
# so we need to convert qubo to serializable object
qubo_edges = [[i, j] for i, j in q.keys()]
qubo_vales = [q[i, j] for i, j in qubo_edges]
exp.log_object('qubo', {'qubo_edges': qubo_edges, 'qubo_vales': qubo_vales})
beta_min_list = [schedule['beta_min'], 0.1, 1.0, 2.0, 3.0, 4.0, 5.0]
beta_max_list = [10.0, 20, 30.0, 40.0, 50.0, 12404, schedule['beta_max']]
num_reads = 300
exp.log_parameter('num_reads', num_reads)
for beta_min in beta_min_list:
for beta_max in beta_max_list:
with exp.run():
sampler = oj.SASampler()
response = exp.log_solver(sampler.sample_qubo)(q, num_reads=num_reads, beta_min=beta_min, beta_max=beta_max)
exp.log_object('response', response.to_serializable())
energies = response.energies
exp.log_parameter('mean_energy', np.mean(energies))
exp.log_parameter('std_energy', np.std(energies))
exp.log_parameter('min_energy', np.min(energies))
exp.log_parameter('exec_time', response.info['execution_time'])
run_table = exp.get_run_table()
run_table
| parameter | metadata | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| solver_name | num_reads | beta_min | beta_max | mean_energy | std_energy | min_energy | exec_time | run_id | elapsed_time | |
| run_id | ||||||||||
| 0 | sample_qubo | 300 | 0.033952 | 10.000000 | -513.646088 | 0.213896 | -513.880988 | 9705.393203 | 0 | 6.049397 |
| 1 | sample_qubo | 300 | 0.033952 | 20.000000 | -513.683011 | 0.195517 | -513.880988 | 8305.705551 | 1 | 5.164798 |
| 2 | sample_qubo | 300 | 0.033952 | 30.000000 | -513.701567 | 0.181375 | -513.880988 | 7795.905981 | 2 | 4.826093 |
| 3 | sample_qubo | 300 | 0.033952 | 40.000000 | -513.685011 | 0.196573 | -513.880988 | 7553.232955 | 3 | 4.672791 |
| 4 | sample_qubo | 300 | 0.033952 | 50.000000 | -513.691557 | 0.196815 | -513.880988 | 7339.252185 | 4 | 4.597259 |
| 5 | sample_qubo | 300 | 0.033952 | 12404.000000 | -513.662848 | 0.242503 | -513.880988 | 4588.150592 | 5 | 2.881303 |
| 6 | sample_qubo | 300 | 0.033952 | 146262.078051 | -513.646933 | 0.216257 | -513.880988 | 3924.553880 | 6 | 2.509776 |
| 7 | sample_qubo | 300 | 0.100000 | 10.000000 | -513.656759 | 0.237213 | -513.880988 | 6301.054997 | 7 | 3.932679 |
| 8 | sample_qubo | 300 | 0.100000 | 20.000000 | -513.691143 | 0.187984 | -513.880988 | 5589.342063 | 8 | 3.529243 |
| 9 | sample_qubo | 300 | 0.100000 | 30.000000 | -513.707417 | 0.186051 | -513.880988 | 5251.696403 | 9 | 3.313255 |
| 10 | sample_qubo | 300 | 0.100000 | 40.000000 | -513.708179 | 0.201705 | -513.880988 | 5101.630311 | 10 | 3.295773 |
| 11 | sample_qubo | 300 | 0.100000 | 50.000000 | -513.716929 | 0.199913 | -513.880988 | 4887.055428 | 11 | 3.084042 |
| 12 | sample_qubo | 300 | 0.100000 | 12404.000000 | -513.649495 | 0.257786 | -513.880988 | 3067.419454 | 12 | 2.000824 |
| 13 | sample_qubo | 300 | 0.100000 | 146262.078051 | -513.673241 | 0.223819 | -513.880988 | 2622.175164 | 13 | 1.718116 |
| 14 | sample_qubo | 300 | 1.000000 | 10.000000 | -513.667470 | 0.210575 | -513.880988 | 1492.951692 | 14 | 1.058311 |
| 15 | sample_qubo | 300 | 1.000000 | 20.000000 | -513.695942 | 0.183224 | -513.880988 | 1361.964409 | 15 | 0.962639 |
| 16 | sample_qubo | 300 | 1.000000 | 30.000000 | -513.713585 | 0.188009 | -513.880988 | 1288.835031 | 16 | 0.922369 |
| 17 | sample_qubo | 300 | 1.000000 | 40.000000 | -513.692656 | 0.170863 | -513.880988 | 1262.007928 | 17 | 0.903518 |
| 18 | sample_qubo | 300 | 1.000000 | 50.000000 | -513.706433 | 0.187874 | -513.880988 | 1232.389053 | 18 | 0.887210 |
| 19 | sample_qubo | 300 | 1.000000 | 12404.000000 | -513.684895 | 0.199205 | -513.880988 | 1006.960931 | 19 | 0.753041 |
| 20 | sample_qubo | 300 | 1.000000 | 146262.078051 | -513.672631 | 0.204222 | -513.880988 | 968.349322 | 20 | 0.732900 |
| 21 | sample_qubo | 300 | 2.000000 | 10.000000 | -513.674988 | 0.203544 | -513.880988 | 1145.799743 | 21 | 0.836082 |
| 22 | sample_qubo | 300 | 2.000000 | 20.000000 | -513.724817 | 0.179151 | -513.880988 | 1071.336251 | 22 | 0.790597 |
| 23 | sample_qubo | 300 | 2.000000 | 30.000000 | -513.725198 | 0.167566 | -513.880988 | 1037.448087 | 23 | 0.775524 |
| 24 | sample_qubo | 300 | 2.000000 | 40.000000 | -513.726547 | 0.167947 | -513.880988 | 1018.720421 | 24 | 0.758649 |
| 25 | sample_qubo | 300 | 2.000000 | 50.000000 | -513.709340 | 0.170286 | -513.880988 | 1019.319887 | 25 | 0.756488 |
| 26 | sample_qubo | 300 | 2.000000 | 12404.000000 | -513.691366 | 0.211648 | -513.880988 | 906.133748 | 26 | 0.691349 |
| 27 | sample_qubo | 300 | 2.000000 | 146262.078051 | -513.687734 | 0.214674 | -513.880988 | 886.778601 | 27 | 0.731327 |
| 28 | sample_qubo | 300 | 3.000000 | 10.000000 | -513.685860 | 0.188711 | -513.880988 | 1047.303160 | 28 | 0.776400 |
| 29 | sample_qubo | 300 | 3.000000 | 20.000000 | -513.723616 | 0.167433 | -513.880988 | 985.388480 | 29 | 0.739154 |
| 30 | sample_qubo | 300 | 3.000000 | 30.000000 | -513.725525 | 0.171873 | -513.880988 | 962.449584 | 30 | 0.725511 |
| 31 | sample_qubo | 300 | 3.000000 | 40.000000 | -513.718090 | 0.179684 | -513.880988 | 950.230960 | 31 | 0.721308 |
| 32 | sample_qubo | 300 | 3.000000 | 50.000000 | -513.720097 | 0.189601 | -513.880988 | 942.807194 | 32 | 0.713487 |
| 33 | sample_qubo | 300 | 3.000000 | 12404.000000 | -513.729398 | 0.210266 | -513.880988 | 879.542348 | 33 | 0.674231 |
| 34 | sample_qubo | 300 | 3.000000 | 146262.078051 | -513.675086 | 0.354749 | -513.880988 | 863.107779 | 34 | 0.671187 |
| 35 | sample_qubo | 300 | 4.000000 | 10.000000 | -513.681077 | 0.212771 | -513.880988 | 997.681382 | 35 | 0.743504 |
| 36 | sample_qubo | 300 | 4.000000 | 20.000000 | -513.750501 | 0.165460 | -513.880988 | 950.550270 | 36 | 0.717235 |
| 37 | sample_qubo | 300 | 4.000000 | 30.000000 | -513.767667 | 0.182406 | -513.880988 | 926.490307 | 37 | 0.710626 |
| 38 | sample_qubo | 300 | 4.000000 | 40.000000 | -513.771701 | 0.165880 | -513.880988 | 915.967495 | 38 | 0.697280 |
| 39 | sample_qubo | 300 | 4.000000 | 50.000000 | -513.769045 | 0.173049 | -513.880988 | 920.349023 | 39 | 0.698451 |
| 40 | sample_qubo | 300 | 4.000000 | 12404.000000 | -513.672979 | 0.456536 | -513.880988 | 863.674593 | 40 | 0.670464 |
| 41 | sample_qubo | 300 | 4.000000 | 146262.078051 | -513.556963 | 0.717156 | -513.880988 | 855.016649 | 41 | 0.794490 |
| 42 | sample_qubo | 300 | 5.000000 | 10.000000 | -513.723920 | 0.185922 | -513.880988 | 970.369341 | 42 | 0.727682 |
| 43 | sample_qubo | 300 | 5.000000 | 20.000000 | -513.764570 | 0.163447 | -513.880988 | 926.980539 | 43 | 0.704735 |
| 44 | sample_qubo | 300 | 5.000000 | 30.000000 | -513.786749 | 0.167871 | -513.880988 | 906.887357 | 44 | 0.691428 |
| 45 | sample_qubo | 300 | 5.000000 | 40.000000 | -513.758803 | 0.215259 | -513.880988 | 911.303211 | 45 | 0.691621 |
| 46 | sample_qubo | 300 | 5.000000 | 50.000000 | -513.752981 | 0.234937 | -513.880988 | 896.117907 | 46 | 0.685812 |
| 47 | sample_qubo | 300 | 5.000000 | 12404.000000 | -513.521661 | 0.637746 | -513.880988 | 858.492901 | 47 | 0.663451 |
| 48 | sample_qubo | 300 | 5.000000 | 146262.078051 | -513.388921 | 0.912442 | -513.880988 | 860.130109 | 48 | 0.662643 |
4. Visualizing the results#
Convert the run_table to a format suitable for heatmap visualization using pivot method.
MINTO’s .get_run_table() returns a DataFrame with double-header, so we use 'parameter' key
to extract the relevant DataFrame and then transform it for heatmap visualization.
param_table = run_table['parameter'].pivot(index='beta_min', columns='beta_max', values='mean_energy')
param_table
| beta_max | 1.000000e+01 | 2.000000e+01 | 3.000000e+01 | 4.000000e+01 | 5.000000e+01 | 1.240400e+04 | 1.095377e+06 |
|---|---|---|---|---|---|---|---|
| beta_min | |||||||
| 0.035392 | -453.464982 | -453.507494 | -453.534059 | -453.532953 | -453.519391 | -453.501373 | -453.501622 |
| 0.100000 | -453.453971 | -453.529594 | -453.524856 | -453.537001 | -453.511809 | -453.510465 | -453.469833 |
| 1.000000 | -453.459997 | -453.538323 | -453.551997 | -453.553772 | -453.543713 | -453.530421 | -453.514144 |
| 2.000000 | -453.457537 | -453.544244 | -453.543310 | -453.541399 | -453.548270 | -453.529462 | -453.405491 |
| 3.000000 | -453.410358 | -453.459166 | -453.372327 | -453.351138 | -453.383562 | -453.249898 | -453.131773 |
| 4.000000 | -453.207369 | -453.222023 | -453.382031 | -453.077857 | -453.106334 | -452.971615 | -453.025248 |
| 5.000000 | -453.152222 | -453.051467 | -453.185958 | -453.192416 | -453.218520 | -452.893875 | -452.744779 |
sns.heatmap(param_table, annot=True, fmt='1.2f', cmap='coolwarm')
plt.xlabel('beta_max')
plt.ylabel('beta_min')
plt.title('mean energy')
plt.show()
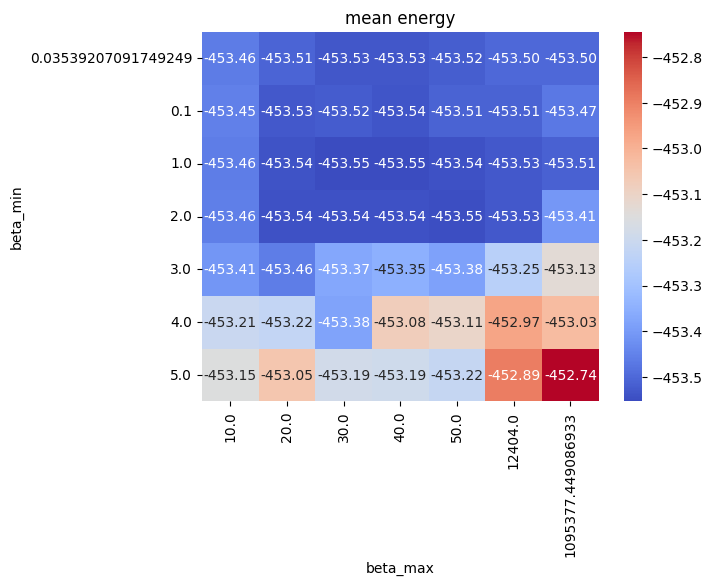
5. Result Analysis#
Looking at the results, OpenJij’s default parameters are not bad, but there appears to be more optimal parameters around beta_max=40.0, beta_min=0.1.
Let’s examine another perspective. In OpenJij’s algorithm, when a spin flip is rejected, no calculation is performed. When a spin flip occurs, the energy difference is calculated. Therefore, if the temperature is high (inverse temperature beta is low) for a long period, the number of spin flips increases, leading to increased computation time.
As a result, the computation time varies depending on the temperature settings. Let’s visualize these results. OpenJij’s computation time is measured in microseconds.
exec_table = run_table["parameter"].pivot(
index="beta_min", columns="beta_max", values="exec_time"
)
sns.heatmap(exec_table, annot=True, fmt="1.2f", cmap="coolwarm")
plt.xlabel("beta_max")
plt.ylabel("beta_min")
plt.title("Execution time")
plt.show()
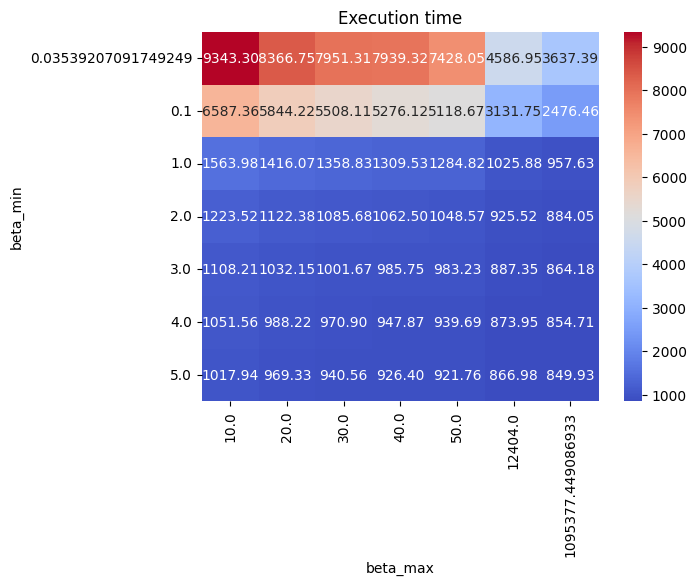
Analysis of OpenJij’s Default Parameters#
Unfortunately, OpenJij’s default parameters (v0.9.1) appear to be suboptimal in terms of computation time.
The temperature parameters are also affected by the num_sweeps parameter that controls the number of steps in simulated annealing.
This numerical experiment reveals that there is still room for improvement in OpenJij’s temperature parameter settings.
MINTO proves useful in gaining insights about solver parameter configurations.
