水素分子のための変分量子固有値ソルバー(VQE)#
このチュートリアルでは、水素分子(H₂)の基底状態エネルギーを求めるための変分量子固有値ソルバー(VQE)アルゴリズムの実装について解説します。分子ハミルトニアンの生成にはOpenFermion、量子回路の構築にはQamomile、量子シミュレーションにはQiskitなど、さまざまな量子コンピューティングフレームワークを使用します。
ワークフローは以下の通りです:
分子ハミルトニアンを量子ビット演算子へ変換
パラメータ化された量子回路(アンザッツ)の作成
VQEによる最適化の実装
原子間距離ごとのエネルギー地形の解析
量子コンピューティングを用いて量子化学の問題を解く方法を示し、特にH₂分子の最小エネルギー構造の探索に焦点を当てます。
# 必要なパッケージは以下のコマンドでインストールできます
# !pip install openfermion pyscf openfermionpyscf
import matplotlib.pyplot as plt
import numpy as np
import openfermion.chem as of_chem
import openfermion.transforms as of_trans
import openfermionpyscf as of_pyscf
import qiskit as qk
import qiskit.primitives as qk_pr
from qiskit_aer import AerSimulator
from qiskit_aer.primitives import EstimatorV2
from scipy.optimize import minimize
from qamomile.core.ansatz.efficient_su2 import create_efficient_su2_circuit
from qamomile.core.circuit.drawer import plot_quantum_circuit
import qamomile.core.operator as qm_o
import qamomile.qiskit as qm_qk
水素分子のハミルトニアンの作成#
basis = "sto-3g"
multiplicity = 1
charge = 0
distance = 0.977
geometry = [["H", [0, 0, 0]], ["H", [0, 0, distance]]]
description = "tmp"
molecule = of_chem.MolecularData(geometry, basis, multiplicity, charge, description)
molecule = of_pyscf.run_pyscf(molecule, run_scf=True, run_fci=True)
n_qubit = molecule.n_qubits
n_electron = molecule.n_electrons
fermionic_hamiltonian = of_trans.get_fermion_operator(molecule.get_molecular_hamiltonian())
jw_hamiltonian = of_trans.jordan_wigner(fermionic_hamiltonian)
Qamomile ハミルトニアンへの変換#
このセクションでは、OpenFermionのハミルトニアンをQamomileフォーマットに変換する。 まず、Jordan-Wigner変換を適用してフェルミ粒子演算子を量子ビット演算子へ変換し、その後、カスタム変換関数を用いてQamomileに適したハミルトニアン表現を作成する。
def operator_to_qamomile(operators: tuple[tuple[int, str], ...]) -> qm_o.Hamiltonian:
pauli = {"X": qm_o.X, "Y": qm_o.Y, "Z": qm_o.Z}
H = qm_o.Hamiltonian()
H.constant = 1.0
for ope in operators:
H = H * pauli[ope[1]](ope[0])
return H
def openfermion_to_qamomile(of_h) -> qm_o.Hamiltonian:
H = qm_o.Hamiltonian()
for k, v in of_h.terms.items():
if len(k) == 0:
H.constant += v
else:
H += operator_to_qamomile(k) * v
return H
hamiltonian = openfermion_to_qamomile(jw_hamiltonian)
VQE アンザッツの作成#
このセクションでは、VQEアルゴリズムのための簡単なアンザッツを作成する。 アンザッツとは、試行波動関数を準備するパラメータ付き量子回路である。 ここでは、Qamomileフレームワークを用いてアンザッツ回路を構築する。
ansatz = create_efficient_su2_circuit(
hamiltonian.num_qubits, rotation_blocks=["ry", "rz"],
reps=4, entanglement="linear"
)
plot_quantum_circuit(ansatz)

Qiskitを用いたVQEの実行#
このセクションでは、QamomileのハミルトニアンとアンザッツをQiskitフォーマットに変換した後、Qiskit Aerシミュレータを用いてVQEを実行する。もちろん、他の量子コンピューティングフレームワークを使用することも可能である。
qk_transpiler = qm_qk.QiskitTranspiler()
qk_ansatz = qk_transpiler.transpile_circuit(ansatz)
qk_hamiltonian = qk_transpiler.transpile_hamiltonian(hamiltonian)
# !pip install qiskit-aer
cost_history = []
aer_sim = AerSimulator()
qk_circuit_transpiled_ansatz = qk.transpile(qk_ansatz, aer_sim)
estimator = EstimatorV2()
def cost_estimator(param_values):
job = estimator.run([(qk_ansatz, qk_hamiltonian, param_values)])
result = job.result()[0]
cost = result.data["evs"]
return cost
def cost_callback(param_values):
cost_history.append(cost_estimator(param_values))
initial_params = np.random.uniform(0, np.pi, len(qk_ansatz.parameters))
# QAOA最適化を実行する
result = minimize(
cost_estimator,
initial_params,
method="BFGS",
options={"disp": True, "maxiter": 50, "gtol": 1e-6},
callback=cost_callback
)
print(result)
Current function value: -1.105868
Iterations: 50
Function evaluations: 2091
Gradient evaluations: 51
message: Maximum number of iterations has been exceeded.
success: False
status: 1
fun: -1.1058675315265363
x: [ 3.157e+00 2.124e+00 ... 1.591e+00 4.345e-01]
nit: 50
jac: [ 5.545e-05 1.662e-04 ... 5.196e-04 -2.392e-05]
hess_inv: [[ 6.494e+00 -2.618e+00 ... 1.032e+01 -6.820e-01]
[-2.618e+00 9.130e+00 ... -5.761e+00 3.409e+00]
...
[ 1.032e+01 -5.761e+00 ... 2.391e+01 -1.763e+00]
[-6.820e-01 3.409e+00 ... -1.763e+00 2.796e+00]]
nfev: 2091
njev: 51
/Users/yuyamashiro/Library/Caches/pypoetry/virtualenvs/qamomile-s0Pfpxir-py3.10/lib/python3.10/site-packages/scipy/optimize/_minimize.py:726: OptimizeWarning: Maximum number of iterations has been exceeded.
res = _minimize_bfgs(fun, x0, args, jac, callback, **options)
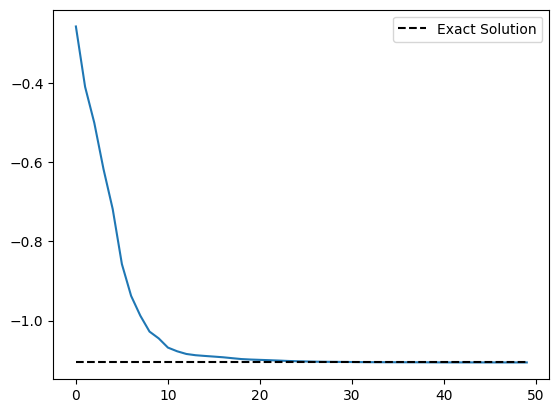
plt.plot(cost_history)
plt.plot(
range(len(cost_history)),
[molecule.fci_energy] * len(cost_history),
linestyle="dashed",
color="black",
label="Exact Solution",
)
plt.legend()
plt.show()
原子同士の距離を変更する#
def hydrogen_molecule(bond_length):
basis = "sto-3g"
multiplicity = 1
charge = 0
geometry = [["H", [0, 0, 0]], ["H", [0, 0, bond_length]]]
description = "tmp"
molecule = of_chem.MolecularData(geometry, basis, multiplicity, charge, description)
molecule = of_pyscf.run_pyscf(molecule, run_scf=True, run_fci=True)
n_qubit = molecule.n_qubits
n_electron = molecule.n_electrons
fermionic_hamiltonian = of_trans.get_fermion_operator(
molecule.get_molecular_hamiltonian()
)
jw_hamiltonian = of_trans.jordan_wigner(fermionic_hamiltonian)
return openfermion_to_qamomile(jw_hamiltonian), molecule.fci_energy
bond_lengths = np.linspace(0.2, 1.5, 15)
energies = []
for bond_length in bond_lengths:
hamiltonian, fci_energy = hydrogen_molecule(bond_length)
ansatz = create_efficient_su2_circuit(
hamiltonian.num_qubits, rotation_blocks=["ry", "rz"],
reps=4, entanglement="linear"
)
qk_ansatz = qk_transpiler.transpile_circuit(ansatz)
qk_hamiltonian = qk_transpiler.transpile_hamiltonian(hamiltonian)
cost_history = []
initial_params = np.random.uniform(0, np.pi, len(qk_ansatz.parameters))
result = minimize(
cost_estimator,
initial_params,
method="BFGS",
options={"maxiter": 50, "gtol": 1e-6},
)
energies.append(result.fun)
print("distance: ", bond_length, "energy: ", result.fun, "fci_energy: ", fci_energy)
distance: 0.2 energy: 0.15754119488608387 fci_energy: 0.15748213479836348
distance: 0.29285714285714287 energy: -0.5679350331466697 fci_energy: -0.5679447209710022
distance: 0.38571428571428573 energy: -0.8833020521044717 fci_energy: -0.8833596636183383
distance: 0.4785714285714286 energy: -1.0335991644424345 fci_energy: -1.0336011797110967
distance: 0.5714285714285714 energy: -1.1035710721430323 fci_energy: -1.1042094222435161
distance: 0.6642857142857144 energy: -1.1322058758760072 fci_energy: -1.132350882707551
distance: 0.7571428571428571 energy: -1.136784862771528 fci_energy: -1.1369026717971324
distance: 0.8500000000000001 energy: -1.1281267827080066 fci_energy: -1.1283618784581124
distance: 0.9428571428571428 energy: -1.1125670649192354 fci_energy: -1.1127252078468768
distance: 1.0357142857142858 energy: -1.093269672823594 fci_energy: -1.0934760882294043
distance: 1.1285714285714286 energy: -1.0725622262836512 fci_energy: -1.0727578805453502
distance: 1.2214285714285713 energy: -1.0519588130652564 fci_energy: -1.0520081621708446
distance: 1.3142857142857143 energy: -1.0322273864176297 fci_energy: -1.032240030624708
distance: 1.4071428571428573 energy: -1.0137141437663768 fci_energy: -1.014147058669549
distance: 1.5 energy: -0.9978997023749084 fci_energy: -0.9981493534714101
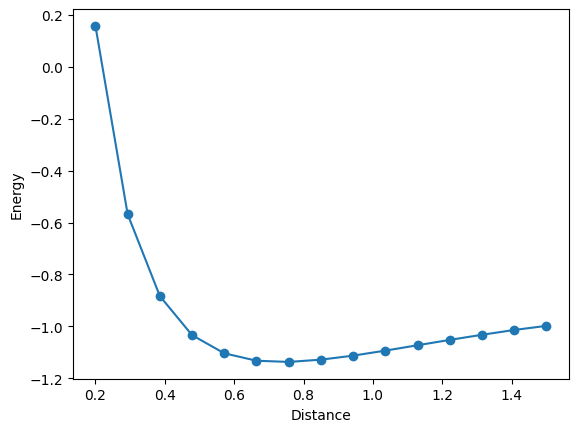
plt.plot(bond_lengths, energies, "-o")
plt.xlabel("Distance")
plt.ylabel("Energy")
plt.show()