頂点被覆問題#
このセクションでは、JijModelingとQamomileライブラリを用いて、QAOAを使って頂点被覆問題を解いていきます。
まずは、使用する主要なライブラリをインストールおよびインポートしましょう。
# !pip install qamomile[qiskit,quri-parts]
# !pip install pylatexenc
from collections import defaultdict
import jijmodeling as jm
import matplotlib.pyplot as plt
import numpy as np
import networkx as nx
import ommx.v1
import qiskit as qk
import qiskit.primitives as qk_pr
from qiskit_aer import AerSimulator
from qiskit_aer.primitives import EstimatorV2
from scipy.optimize import minimize
import qamomile.core as qm
from qamomile.core.circuit.drawer import plot_quantum_circuit
import qamomile.qiskit as qm_qk
数理モデルの構築#
頂点被覆問題の定式化を考えてみましょう。2値変数 \(x_i\) を定義し、頂点 \(i\) が集合 \(S\) に含まれる場合は \(x_i = 1\)、含まれない場合は \(x_i = 0\) とします。集合 \(S\) のサイズを表す目的関数は、以下のように表されます。
制約条件は、すべての辺が被覆されていることであり、つまり各辺に対して、その両端点のうち少なくとも一方が集合 \(S\) に含まれている必要があります。これは次のように定式化できます。
まとめると、頂点被覆問題は次のように定式化できます。
上記の定式化を記述し、それを基にJijModelingを使って問題モデルを作成します。Placeholderはデータとして代入される値を定義し、BinaryVarは意思決定変数を定義し、Elementは総和に使われる添字を定義します。出力を確認することで、定式化が正しいことを確認できます。
def vertex_cover_problem() -> jm.Problem:
# 変数を定義する
V = jm.Placeholder("V")
E = jm.Placeholder("E", ndim=2)
x = jm.BinaryVar("x", shape=(V,))
i = jm.Element("i", belong_to=(0, V))
e = jm.Element("e", belong_to=E)
# 問題を定義する
problem = jm.Problem("Vertex Cover Problem")
# 各辺の少なくとも一方の頂点が被覆に含まれるようにする
# problem += jm.Constraint("cover", x[e[0]] + x[e[1]] >= 1, forall=e)
# 被覆に含まれる頂点の数を最小化する
problem += jm.sum(i, x[i]) + jm.sum(e, (x[e[0]] + x[e[1] - 1.5]) ** 2)
return problem
problem = vertex_cover_problem()
problem
インスタンスデータの準備#
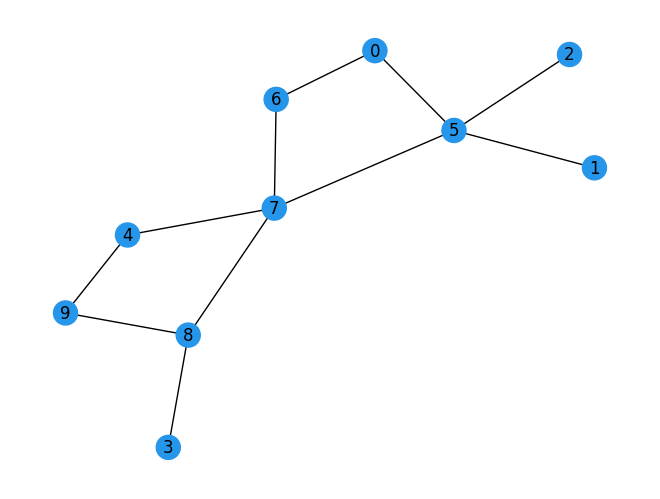
次に、以下のグラフに対して頂点被覆問題を解きます。ここで解こうとしている具体的な問題のデータをインスタンスデータと呼びます。
G = nx.Graph()
G.add_nodes_from([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
G.add_edges_from(
[
(0, 6),
(0, 5),
(1, 5),
(2, 5),
(3, 8),
(4, 9),
(4, 7),
(5, 7),
(6, 7),
(7, 8),
(8, 9),
]
)
positions = nx.spring_layout(G)
color = ["#2696EB"] * G.number_of_nodes()
nx.draw(G, node_color=color, pos=positions, with_labels=True)
コンパイル済みインスタンスの作成#
先ほど作成した定式化とインスタンスデータを用いて、JijModeling.Interpreterとommx.Instanceによってコンパイルを行います。この処理によって、インスタンスデータが代入された中間表現が得られます。
inst_E = [list(edge) for edge in G.edges]
num_nodes = G.number_of_nodes()
instance_data = {"V": num_nodes, "E": inst_E}
num_qubits = num_nodes
compiled_instance = jm.Interpreter(instance_data).eval_problem(problem)
Qamomileを用いたQAOA回路とハミルトニアンの生成#
コンパイル済みインスタンスから、QAOA回路とハミルトニアンを生成します。これには qm.qaoa.QAOAConverter を使用します。このクラスのインスタンスを作成し、ising_encodeを使用することで、内部的にIsingハミルトニアンを生成できます。QUBOへの変換時に現れるパラメータはここで設定可能ですが、設定しなければデフォルト値が使用されます。
Isingハミルトニアンが生成された後、get_qaoa_ansatzおよびget_cost_hamiltonianメソッドを使用して、それぞれQAOAの量子回路とハミルトニアンを生成できます。ここではQAOAのレイヤー数 \(p\) を \(3\) に固定します。
qaoa_converter = qm.qaoa.QAOAConverter(compiled_instance)
# Isingハミルトニアンへのエンコードを行う
qaoa_converter.ising_encode()
# QAOA回路を取得する
qaoa_circuit = qaoa_converter.get_qaoa_ansatz(p=3)
# コストハミルトニアンを取得する
qaoa_hamiltonian = qaoa_converter.get_cost_hamiltonian()
QAOA回路の可視化#
Qamomileは量子回路を可視化するためのメソッドを提供しています。plot_quantum_circuit関数を使用することで、QAOAの量子回路を可視化することができます。
plot_quantum_circuit(qaoa_circuit)
取得したQAOA回路とハミルトニアンをQiskit向けに変換#
ここでは、qamomile.qiskit.QiskitTranspilerのコンバータを使用して、Qiskit用のQAOA回路とハミルトニアンを生成します。QiskitTranspiler.transpile_circuitおよび QiskitTranspiler.transpile_hamiltonianという2つのメソッドを使用することで、QAOA回路とハミルトニアンをQiskitで利用可能な形式に変換できます。これにより、Qiskitの量子計算フレームワークを活用して実行および解析が可能になります。
qk_transpiler = qm_qk.QiskitTranspiler()
# QAOA回路をQiskitにトランスパイルする
qk_circuit = qk_transpiler.transpile_circuit(qaoa_circuit)
# QAOAハミルトニアンをQiskitにトランスパイルする
qk_hamiltonian = qk_transpiler.transpile_hamiltonian(qaoa_hamiltonian)
qk_hamiltonian
SparsePauliOp(['IIIIIIIIIZ', 'IIIIIIZIII', 'IIIIIZIIII', 'IIIIIIIIZI', 'IIIIIIIZII', 'IIIZIIIIII', 'IIIIZIIIII', 'IIZIIIIIII', 'IZIIIIIIII', 'ZIIIIIIIII', 'IIIIIIZIIZ', 'IIIIIZIIIZ', 'IIIIIIZIZI', 'IIIIIIZZII', 'IIIZIIZIII', 'IIIIZZIIII', 'IIZIIZIIII', 'IIIZZIIIII', 'IIZZIIIIII', 'IZZIIIIIII', 'IIIIIIIIII'],
coeffs=[-2.5+0.j, -4.5+0.j, -3.5+0.j, -1.5+0.j, -1.5+0.j, -3.5+0.j, -4.5+0.j,
-3.5+0.j, -1.5+0.j, -0.5+0.j, 0.5+0.j, 0.5+0.j, 0.5+0.j, 0.5+0.j,
0.5+0.j, 0.5+0.j, 0.5+0.j, 0.5+0.j, 0.5+0.j, 0.5+0.j, 22. +0.j])
QAOAの実行#
QAOAを実行してパラメータの最適化を行います。ここでは、最適化アルゴリズムとしてCOBYLAを使用します。
cost_history = []
aer_sim = AerSimulator()
qk_circuit = qk.transpile(qk_circuit, aer_sim)
estimator = EstimatorV2()
# コスト推定関数
def estimate_cost(param_values):
job = estimator.run([(qk_circuit, qk_hamiltonian, param_values)])
result = job.result()[0]
cost = result.data["evs"]
cost_history.append(cost)
return cost
# QAOAの初期パラメータ
initial_params = [
np.pi / 8,
np.pi / 4,
3 * np.pi / 8,
np.pi / 2,
np.pi / 2,
3 * np.pi / 8,
]
# COBYLAを用いたQAOAの最適化実行
result = minimize(
estimate_cost,
initial_params,
method="COBYLA",
options={"maxiter": 1500},
)
print(result)
message: Optimization terminated successfully.
success: True
status: 1
fun: 10.382266563384672
x: [ 1.593e+00 8.375e-01 1.131e+00 1.686e+00 1.348e+00
7.099e-01]
nfev: 270
maxcv: 0.0
結果の可視化#
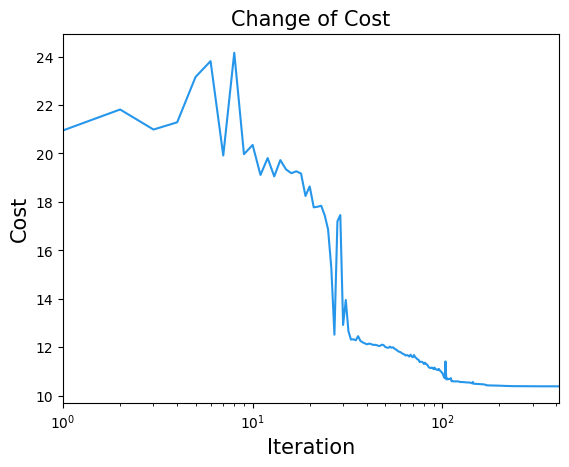
最適化を繰り返すことで、エネルギーが減少して収束していく様子を観察できます。
plt.title("Change of Cost", fontsize=15)
plt.xlabel("Iteration", fontsize=15)
plt.ylabel("Cost", fontsize=15)
plt.xscale("log")
plt.xlim(1, result.nfev)
plt.plot(cost_history, label="Cost", color="#2696EB")
plt.show()
最適化されたパラメータを用いて、Qiskit の StatevectorSampler を実行してみましょう。
# 最適化されたQAOA回路の実行
sampler = qk_pr.StatevectorSampler()
qk_circuit.measure_all()
job = sampler.run([(qk_circuit, result.x)], shots=1000)
job_result = job.result()[0]
qaoa_counts = job_result.data["meas"]
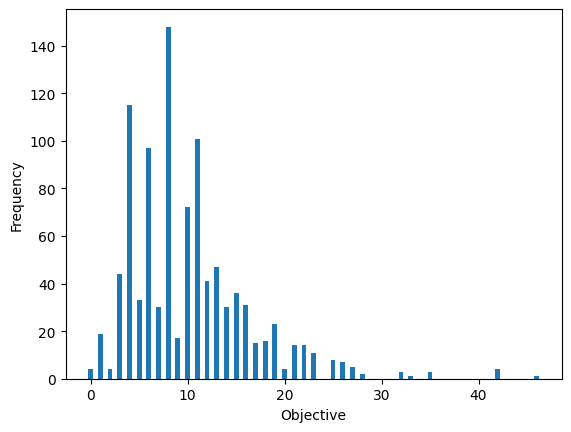
結果の評価#
先ほど取得したジョブカウントから、qaoa_converter.decodeを使ってsamplesetに変換します。samplesetでは実行可能な解（制約を満たす解）のみを選択することができ、目的関数値の分布を確認することができます。
sampleset = qaoa_converter.decode(qk_transpiler, job_result.data["meas"])
# 各エネルギー値の出現回数を蓄積するための辞書を初期化
frequencies = defaultdict(int)
# エネルギー値を丸める精度を定義
for entry in sampleset.raw.objectives.entries:
energy = round(entry.value, ndigits = 3)
frequencies[energy] += len(entry.ids)
plt.bar(frequencies.keys(), frequencies.values(), width=0.5)
plt.xlabel('Objective')
plt.ylabel('Frequency')
plt.show()
解のプロット#
得られた結果の中から、目的関数値を最小にする解を選び、それをプロットします。
（オレンジ色の頂点は頂点被覆に含まれる頂点を表しています。）
def plot_graph_coloring(graph: nx.Graph, sampleset: ommx.v1.SampleSet):
# 実行可能な解を抽出
best_sol = sampleset.best_feasible_unrelaxed()
# 頂点の色リストを初期化
node_colors = ["#2696EB"] * instance_data["V"]
# 頂点の色を設定
x_value = best_sol.extract_decision_variables("x")
for t, v in x_value.items():
if v == 1:
node_colors[t[0]] = "#EA9b26"
# 図を作成
nx.draw_networkx(graph, node_color=node_colors, pos=positions, with_labels=True)
plt.show()
plot_graph_coloring(G, sampleset)
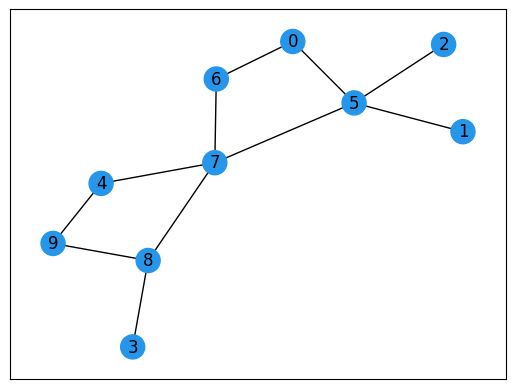
確かに、頂点被覆が得られていることが確認できます。