Shift Optimization Problem#
The shift optimization problem is the problem of finding the optimal cost under several constraints. Here we show an example of shift optimization based on This formulation.
Problem Description#
Overview#
Suppose that we want to allocate multiple jobs to multiple workers. You have to pay a cost per worker. Given the start time and end time of each job and the costs of each worker, minimize the workers’ cost under the constraints;
Each job needs one worker
A worker cannot do multiple jobs at the same time
The figure below is a picture of the shift optimization problem.
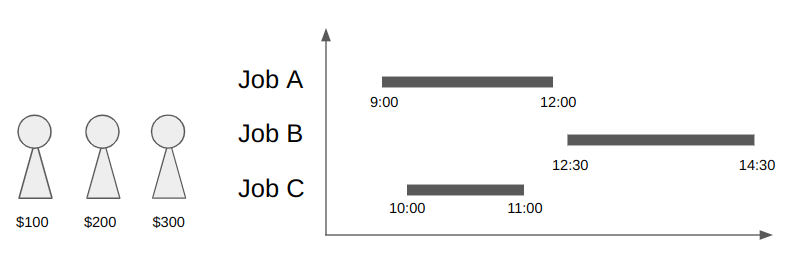
There are three jobs and three workers in this situation. Since job A and B have no overlap. One worker can do these jobs, costing a total $300.
Pre-process#
Before constructing a mathematical model, we list overlapping jobs from the given job schedule. First, we prepare the job scheduling data (list of (start_time, end_time)):
from datetime import time
job_list = [
(time(17, 0), time(18, 0)), # job 0
(time(13, 0), time(14, 0)), # job 1
(time(13, 30), time(14, 30)), # job 2
(time(13, 40), time(14, 40)), # job 3
(time(16, 40), time(17, 40)), # job 4
(time(11, 40), time(13, 40)), # job 5
(time(18, 40), time(19, 40)), # job 6
(time(18, 40), time(19, 40)), # job 7
(time(18, 00), time(19, 00)), # job 8
]
To find overlapping jobs, we first create a graph whose node i corresponds to each job job_list[i], and the edge connects overlapping jobs.
We need the networkx library to run the below code.
import networkx as nx
def has_overlap(t1start: time, t1end: time, t2start: time, t2end: time):
return (t1start <= t2start <= t1end) or (t2start <= t1start <= t2end)
def gen_index_graph(time_list: list[tuple[time, time]]) -> nx.Graph:
G = nx.Graph()
for j in range(len(time_list)):
for k in range(j + 1, len(time_list)):
if has_overlap(
time_list[j][0], time_list[j][1], time_list[k][0], time_list[k][1]
):
G.add_edge(j, k)
return G
We can get the list of overlapping jobs by finding cliques from the graph. The function nx.find_cliques can be used for extracting cliques.
g = gen_index_graph(job_list)
job_cliques = []
for c in nx.find_cliques(g):
job_cliques.append(list(set(c)))
print(job_cliques)
[[0, 8], [0, 4], [1, 2, 3, 5], [8, 6, 7]]
For example, job 0 (from 17:00 to 18:00) and job 8 (from 18:00 to 19:00) has overlap at 18:00 hence it listed as [0, 8].
Job 1, 2, 3, 5 are overlapped each other hence it is also listed.
Mathematical Model#
Constants#
We use the following constants:
\(W\): The number of workers (e.g.
5)\(J\): The number of jobs (e.g.
5)\(b_w\): Costs of the worker w. (e.g.
[1,2,3,2,1])\(C\): List of overlapped jobs (e.g.
[[1,4], [4,2,3,5], [2,3]]. Note that \(C_0\) =[1,4], \(C_1\) =[4,2,3,5], \(C_2\) =[2,3])\(Nc\): The number of overlapped jobs (=
len(C))
Decision Variables#
A binary variables \(x_{j,w}\) and \(y_{w}\) are defined as: $\( x_{j,w} = \begin{cases} 1~\text{the worker {\it w} is assigned to the job {\it j}}\\ 0~\text{otherwise}\\ \end{cases} \)$
for all \(j \in \{0, ..., J-1\}\) and \(w \in \{0, ..., W-1\}\).
Objective Functions#
The cost function to be minimized is the total cost of workers:
Constraints#
We first consider two constraints;
Each job needs one worker $\( \sum_w x_{j, w} = 1, ~\forall j \in \{0, ..., J-1\} \)$
A worker cannot do multiple jobs at the same time. In other words, the number of jobs in \(C_c\) that the worker \(w\) is assigned is 0 (if \(y_{w}\) is 0) or 1 (if \(y_{w}\) is 1).
Modeling by JijModeling#
import jijmodeling as jm
W = jm.Placeholder("W")
w = jm.Element("w", belong_to=W)
# jobs
J = jm.Placeholder("J")
j = jm.Element("j", belong_to=J)
# workers cost
b = jm.Placeholder("b", ndim=1)
# list of overlapped jobs
C = jm.Placeholder("C", ndim=2)
# number of cliques
Nc = jm.Placeholder("Nc")
# index for clique
c = jm.Element("c", belong_to=Nc)
l = jm.Element("l", belong_to=C[c])
# decision variables
# 1 if the worker w is assigned, otherwise 0.
y = jm.BinaryVar("y", shape=(W,))
# 1 if the worker w is assigned to job j.
x = jm.BinaryVar("x", shape=(J, W))
problem = jm.Problem("shift schedule")
problem += jm.sum(w, b[w] * y[w])
problem += jm.Constraint("const_do_all_jobs", jm.sum(w, x[j, w]) == 1, forall=[j])
problem += jm.Constraint(
"const_worker_limit", jm.sum(l, x[l, w]) <= y[w], forall=[w, c]
)
problem
Solve by JijZeptSolver#
Let us compute with five workers and five jobs.
workers_costs = [1, 4, 3, 2, 5]
job_list = [
(time(17, 0), time(18, 0)),
(time(13, 0), time(14, 0)),
(time(13, 30), time(14, 30)),
(time(13, 40), time(14, 40)),
(time(16, 40), time(16, 50)),
]
# Pre-process to job_list
g = gen_index_graph(job_list)
job_cliques = []
for c in nx.find_cliques(g):
job_cliques.append(list(set(c)))
instance_data = {
"W": len(workers_costs),
"J": len(job_list),
"b": workers_costs,
"C": job_cliques,
"Nc": len(job_cliques),
}
import jijzept_solver
interpreter = jm.Interpreter(instance_data)
instance = interpreter.eval_problem(problem)
solution = jijzept_solver.solve(instance, time_limit_sec=1.0)
Visualization#
First, let us check the objective (the cost function) of the solution obtained.
solution.objective
6.0
Next, we visualize the assigned work to workers.
import matplotlib.pyplot as plt
def plot_sol(job_list: list[tuple[time, time]], y: list[int], x: list[list[int]]):
factor = 24 / 86400
bar_job_list = [
(
(e1.hour*3600 + e1.minute*60 + e1.second) * factor,
((e2.hour*3600 + e2.minute*60 + e2.second) - (e1.hour*3600 + e1.minute*60 + e1.second)) * factor
)
for e1, e2 in job_list
]
_, ax = plt.subplots()
for i, val in enumerate(y):
if val == 1:
bar = []
for j in range(len(bar_job_list)):
if [j, i] in x:
bar.append(bar_job_list[j])
ax.broken_barh(bar, (10*(i+1)-2.5, 5))
ax.set_xlim(0, 24)
ax.set_xlabel("job schedule time [Hour]")
ax.set_yticks([10*(i+1) for i,_ in enumerate(y)], labels=[f"workers {i}" for i,_ in enumerate(y)]) # Modify y-axis tick labels
ax.grid(True)
plt.show()
df = solution.decision_variables_df
solution_y = df[df["name"] == "y"]["value"].to_list()
solution_x = df[(df["name"] == "x") & (df["value"] == 1)]["subscripts"].to_list()
plot_sol(job_list, solution_y, solution_x)
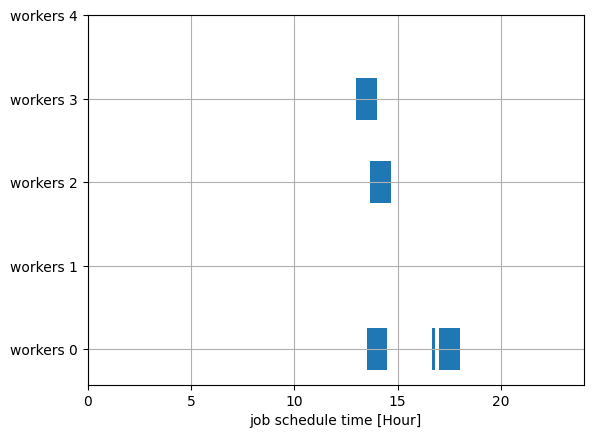
The blue area shows the assigned jobs. We can see that we only need to assign work to workers 0, 2, and 3. Since the wage for worker 0 is 1, for worker 2 is 3, and for worker 3 is 2, the total wage is 1+2+3=6. This assignment results in the minimum total wage.
Other Cases#
Let us consider if all jobs are overlapped.
workers_costs = [1, 4, 3, 2, 5]
job_list = [
(time(10, 10), time(19, 0)),
(time(10, 20), time(19, 0)),
(time(10, 30), time(19, 30)),
(time(10, 0), time(19, 40)),
(time(10, 0), time(19, 50)),
]
# Pre-process to job_list
g = gen_index_graph(job_list)
job_cliques = []
for c in nx.find_cliques(g):
job_cliques.append(list(set(c)))
instance_data = {
"W": len(workers_costs),
"J": len(job_list),
"b": workers_costs,
"C": job_cliques,
"Nc": len(job_cliques),
}
interpreter = jm.Interpreter(instance_data)
instance = interpreter.eval_problem(problem)
solution = jijzept_solver.solve(instance, time_limit_sec=1.0)
df = solution.decision_variables_df
solution_y = df[df["name"] == "y"]["value"].to_list()
solution_x = df[(df["name"] == "x") & (df["value"] == 1)]["subscripts"].to_list()
plot_sol(job_list, solution_y, solution_x)
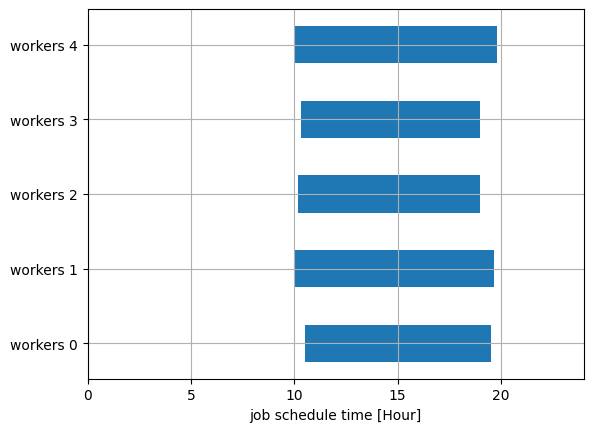
In this case, we need all workers to finish jobs.
