The Clique Problem

The Clique Problem#

Here we show how to solve the clique problem using JijSolver and JijModeling. This problem is also mentioned in 2.3. Clique on Lucas, 2014, “Ising formulations of many NP problems”.

What is the Clique Problem?#

This is a decision problem of whether or not a clique (complete graph) of size \(K\) exists in a given graph.

Complete graphs#

A complete graph is a graph whose two vertices are all adjacent to each other (not including loops or multiple edges). We show two examples below.

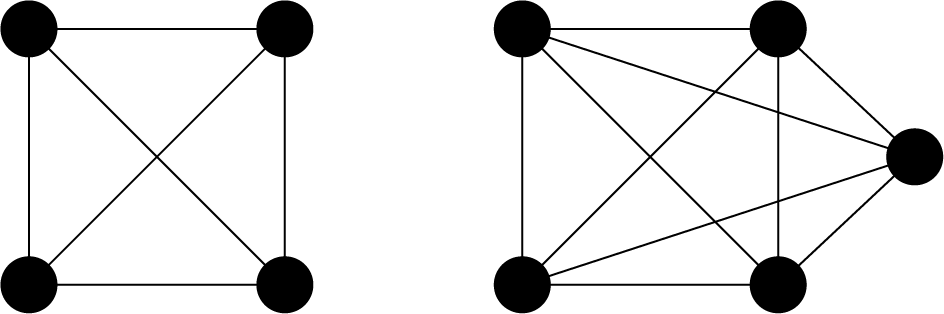
As mentioned above, a vertex in a complete graph is adjacent to all other vertices. A complete undirected graph \(G = (V, E)\) has \({}_V C_2 = \frac{1}{2} V(V-1)\) edges, that is, the number of edges is equal to the number of combinations choosing two vertices from \(V\).

Mathematical Model#

First, we introduce binary variables \(x_{v}\) which are 1 if vertex \(v\) belongs to the subgraph and 0 otherwise.

Constraint 1: sum of \(x_v\) must equal K#

In this problem, each vertex \(x_v\) is 1 if vertex \(v\) is selected as part of the subgraph, and 0 otherwise.

\[ \sum_{v=0}^{V-1} x_{v} = K \tag{1} \]

Constraint 2: The subgraph must be complete#

If the subgraph \(G (W, E_W)\) where \(E_W\) represents the subset of edges \(E\) restricted to those connecting nodes within \(W\), is complete, then the number of edges in this subgraph is given by \(\frac{1}{2} W (W -1)\) from previous discussion. Knowing that the subgraph has \(\sum_{(uv) \in E_W} x_{u} x_{v}\) edges, we set the constraint function as follows.

\[ \sum_{(uv) \in E} x_{u} x_{v} = \frac{1}{2} K(K-1) \tag{2} \]

Modeling by JijModeling#

Next, we show an implementation using JijModeling. We first define variables for the mathematical model described above.

import jijmodeling as jm

# define variables
V = jm.Placeholder('V')
E = jm.Placeholder('E', ndim=2)
K = jm.Placeholder('K')
x = jm.BinaryVar('x', shape=(V,))
u = jm.Element('u', (V))
e = jm.Element('e', E)

We use the same variables in the graph partitioning problem, and we add \(K\) to that.

Constraint 1#

We implement the constraint, Equation (1).

# set problem
problem = jm.Problem('Clique')
# set constraint: sum of $x_v$ must equal K
problem += jm.Constraint('constraint1', jm.sum(u, x[u])==K)

Constraint 2#

Next, we implement the constraint, Equation (2).

# set constraint: the subgraph must be complete
problem += jm.Constraint('constraint2', jm.sum(e, x[e[0]]*x[e[1]])==1/2*K*(K-1))

Let’s display the implemented mathematical model in Jupyter Notebook.

problem
\[\begin{split}\begin{array}{cccc}\text{Problem:} & \text{Clique} & & \\& & \min \quad \displaystyle 0 & \\\text{{s.t.}} & & & \\ & \text{constraint1} & \displaystyle \sum_{u = 0}^{V - 1} x_{u} = K & \\ & \text{constraint2} & \displaystyle \sum_{e \in E} x_{e_{0}} \cdot x_{e_{1}} = 0.5 \cdot K \cdot \left(K - 1\right) & \\\text{{where}} & & & \\& x & 1\text{-dim binary variable}\\\end{array}\end{split}\]

Prepare an instance#

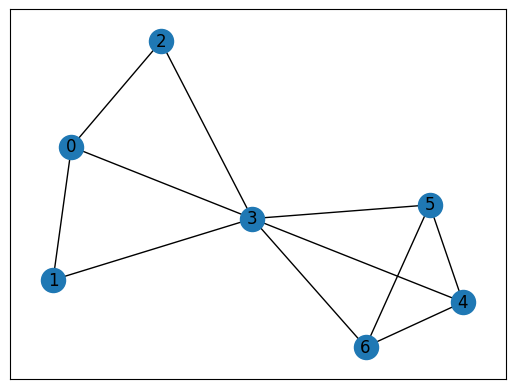
We prepare a graph by using Networkx, focusing on a scenario where the graph includes a complete subgraph of size \(K=4\).

import networkx as nx

# set the number of random vertices
inst_V1 = 3
# create a random graph
inst_G1 = nx.gnp_random_graph(inst_V1, 0.2)

# set the size K
inst_K = 4
# create a complete graph with K vertices
inst_G2 = nx.complete_graph(inst_K)

# set the number of vertices
inst_V = inst_V1 + inst_K

# add the complete graph to the given graph
inst_G = nx.union(inst_G1, inst_G2, rename=('G-', 'K-'))

# connect each vertex of G1 to vertex 0 of G2
for i in range(inst_V1):
    inst_G.add_edge(f'G-{i}', 'K-0')

# relabel the nodes using normal numbers from 0
mapping = {node: i for i, node in enumerate(inst_G.nodes)}
inst_G = nx.relabel_nodes(inst_G, mapping)

# get information of edges
inst_E = [list(edge) for edge in inst_G.edges]

instance_data = {'V': inst_V, 'E': inst_E, 'K': inst_K}

This graph for the clique problem is shown below.

import matplotlib.pyplot as plt

pos = nx.spring_layout(inst_G)
nx.draw_networkx(inst_G, pos, with_labels=True)

plt.show()
../_images/fce3d086776284387c7a92facff6e4956188e83bfce3101d5e23bad6eecf7d49.png

Solve by JijSolver#

We solve this problem using JijSolver.

import jijsolver

interpreter = jm.Interpreter(instance_data)
instance = interpreter.eval_problem(problem)
solution = jijsolver.solve(instance, time_limit_sec=1.0)

Visualize the solution#

In the end, we visualize the solution obtained.

import numpy as np

df = solution.decision_variables
vertices = np.ravel(df[df["value"]==1]["subscripts"].to_list())
print(vertices)
# set color list for visualization
cmap = plt.get_cmap("tab10")
# initialize vertex color list
node_colors = [cmap(0)] * instance_data["V"]
# set the vertex color list
for i in vertices:
    node_colors[i] = cmap(1)
# highlight the edge of clique
highlight_edges = [(u, v) for (u, v) in inst_G.edges() if u in vertices and v in vertices]
# make figure
nx.draw_networkx(inst_G, pos, node_color=node_colors, with_labels=True)
nx.draw_networkx_edges(inst_G, pos, edgelist=highlight_edges, edge_color='red')
plt.show()

[3 4 5 6]
../_images/3890c866c60f1c604fe5f8d36a26df54a5004dce824da8b021f0ac9185fd748f.png

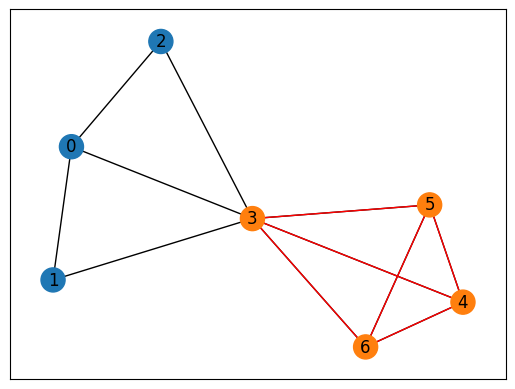
We obtain a feasible clique as shown above.

Lastly, we will introduce a trick to reduce the number of extra spins needed to encode a variable that can take \(N\) values. By defining an integer \(M\), where \(2^M \leq N < 2^{(M+1)}\), \(M+1\) binary variables can be used instead of \(N\) binary variables. This can be applied to solve the NP-hard version of the clique problem, and the resulting number of spins required is \(N +1+\lfloor \log \Delta \rfloor\), where \(\Delta\) represents the maximum degree of the graph being considered in the clique problem. This is mentioned in 2.4. Reducing \(N\) to \(log N\) Spins in Some Constraints on Lucas, 2014, “Ising formulations of many NP problems”.

Contents