Graph Partitioning

Graph Partitioning#

Here we show how to solve the graph partitioning problem using JijSolver and JijModeling. This problem is also mentioned in 2.2. Graph Partitioning on Lucas, 2014, “Ising formulations of many NP problems”.

What is Graph Partitioning?#

Graph partitioning is the problem of dividing a graph into two subsets of equal size with the aim of minimizing the number of edges between the subsets.

Example#

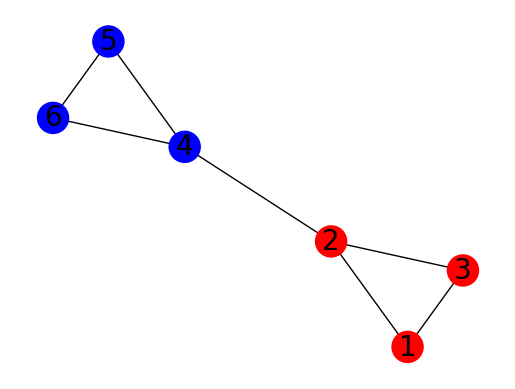
Let us take a look at the following situation. Consider a graph with 6 vertices labeled from 1 to 6, and edges connecting the vertices as follows:

  • 1 is connected to 2 and 3

  • 2 is connected to 1, 3, and 4

  • 3 is connected to 1 and 2

  • 4 is connected to 2, 5, and 6

  • 5 is connected to 4 and 6

  • 6 is connected to 4 and 5

The goal is to partition this graph into two subsets of equal size (i.e., 3 vertices in each subset) with minimized edges between them. In this case, the optimal solution is \(\{1, 2, 3\}, \{4, 5, 6\}\), where there is only 1 edge connecting vertices in different subsets (i.e., the edge (2,4)), which is the minimum possible number of edges connecting the two subsets.

Mathematical Model#

Let \(G=(V, E)\) be the undirected graph where \(V\) is the set of vertices and \(E\) is the set of edges. The goal is to partition \(V\) into two subsets \(V_1\) and \(V_2\) of equal size, with the number of edges crossing the partition being minimized. We introduce variables \(x_{u}\) which is 1 if vertex \(u\) is in the subset \(V_1\) and 0 if vertex \(u\) is in the subset \(V_2\).

Constraint: the vertices must be partitioned into two equal-sized sets

We express this constraint as follows:

\[ ∑_{u \in V} x_u = V/2 \tag{1} \]

Objective function: minimize the number of edges crossing the partition

\[ \min \quad \sum_{(uv) \in E} (\{x_{u} (1-x_{v})\}+\{(1-x_{u}) x_{v}\}) \tag{2} \]

Here, the first term \(x_u (1 - x_v)\) evaluates to 1 if edge (u, v) crosses the boundary between \(V_1\) and \(V_2\) (i.e., if \(u\) belongs to \(V_1\) and \(v\) belongs to \(V_2\)), and 0 otherwise. Similarly, the second term \((1 - x_u) x_v\) evaluates to 1 if edge (u, v) crosses the boundary between \(V_2\) and \(V_1\) (i.e., if \(u\) belongs to \(V_2\) and \(v\) belongs to \(V_1\)), and 0 otherwise. Thus, this objective function is an indicator of how much graph partitioning has been achieved.

Modeling by JijModeling#

Next, we show an implementation using JijModeling. We first define variables for the mathematical model described above.

import jijmodeling as jm

# define variables
V = jm.Placeholder('V')
E = jm.Placeholder('E', ndim=2)
x = jm.BinaryVar('x', shape=(V,))
u = jm.Element('u', belong_to=V)
e = jm.Element('e', belong_to=E)

V=jm.Placeholder('V') represents the number of vertices. We denote E=jm.Placeholder('E', ndim=2) as a set of edges. Then, we define a list of binary variables x=jm.BinaryVar('x', shape=(V,)), and we set the subscripts u used in the mathematical model. Finally, e represents the variable for edges. e[0] and e[1] represent the two vertices connected by the edge.

Constraint#

We implement a constraint, Equation (1).

# set problem
problem = jm.Problem('Graph Partitioning')
# set constraint: the vertices must be partitioined into two equal-sized sets
const = jm.sum(u, x[u])
problem += jm.Constraint('constraint', const==V/2)

Objective function#

Next, we implement an objective function, Equation (2).

# set objective function: minimize the number of edges crossing the partition
A_1 = x[e[0]]*(1-x[e[1]])
A_2 = (1-x[e[0]])*x[e[1]]
problem += jm.sum(e, (A_1 + A_2))

Let’s display the implemented mathematical model in Jupyter Notebook.

problem
\[\begin{split}\begin{array}{cccc}\text{Problem:} & \text{Graph Partitioning} & & \\& & \min \quad \displaystyle \sum_{e \in E} \left(x_{e_{0}} \cdot \left(- x_{e_{1}} + 1\right) + \left(- x_{e_{0}} + 1\right) \cdot x_{e_{1}}\right) & \\\text{{s.t.}} & & & \\ & \text{constraint} & \displaystyle \sum_{u = 0}^{V - 1} x_{u} = V \cdot 2^{(-1)} & \\\text{{where}} & & & \\& x & 1\text{-dim binary variable}\\\end{array}\end{split}\]

Prepare an instance#

We prepare a graph using NetworkX. Here we create a random graph with 12 vertices.

import networkx as nx

# set the number of vertices
inst_V = 12
# create a random graph
inst_G = nx.gnp_random_graph(inst_V, 0.4)
# get information of edges
inst_E = [list(edge) for edge in inst_G.edges]
instance_data = {'V': inst_V, 'E': inst_E}

Solve by JijSolver#

We solve this problem using jijsolver.

import jijsolver

interpreter = jm.Interpreter(instance_data)
instance = interpreter.eval_problem(problem)
solution = jijsolver.solve(instance, time_limit_sec=1.0)

Visualize the solution#

In the end, we visualize the solution obtained.

import matplotlib.pyplot as plt
import numpy as np

df = solution.decision_variables
x_indices = np.ravel(df[df["value"]==1]["subscripts"].to_list())
# set color list for visualization
cmap = plt.get_cmap("tab10")
# initialize vertex color list
node_colors = [cmap(0)] * instance_data["V"]
# set vertex color list
for i in x_indices:
    node_colors[i] = cmap(1)
# make figure
nx.draw_networkx(inst_G, node_color=node_colors, with_labels=True)
plt.show()
../_images/ea13a03d5c9bc5fbc24f90b61da4f3f53719ee141e752762a897b80da62edd61.png

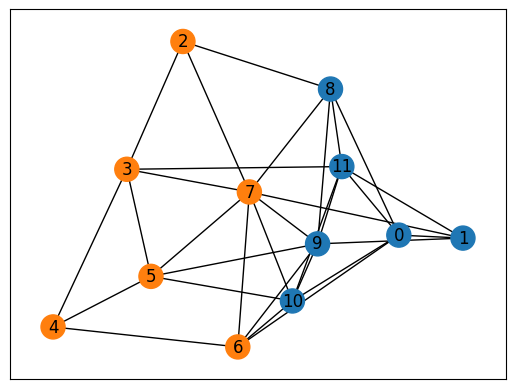
With the above visualization, we obtain a feasible partitioning for this graph.

Contents