Vertex Cover Problem

Vertex Cover Problem#

We show how to solve the vertex cover problem using JijSolver and JijModeling. This problem is also mentioned in 4.3. Vertex Cover on Lucas, 2014, “Ising formulations of many NP problems”.

What is the Vertex Cover Problem?#

The vertex cover problem is defined as follows. Given an undirected graph \(G = (V,E)\), count the smallest number of vertices that can be “colored” such that every edge connects vertices that have different colors from each other. In other words, we want to have a minimum set of vertices that “covers” all the edges in the graph.

For example, consider the following undirected graph:

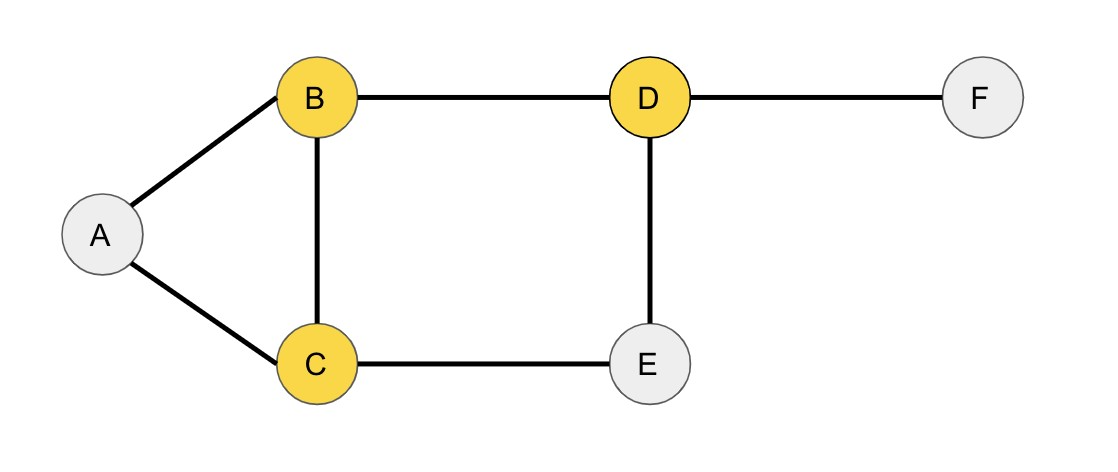
In this graph, the vertices are labeled by A, B, C, D, E, and F, and the edges are expressed by lines connecting the vertices. The vertex cover for this graph is {B, C, D}, which contains at least one vertex from each edge:

  • Edge (A, B) is covered by vertex B

  • Edge (A, C) is covered by vertex C

  • Edge (B, C) is covered by vertices B and C

  • Edge (B, D) is covered by vertices B and D

  • Edge (C, E) is covered by vertex C

  • Edge (D, E) is covered by vertex D

  • Edge (D, F) is covered by vertex D

Mathematical model#

First, we introduce binary variables \(x_{v}\) that take 1 if the vertex \(v\) is colored and take 0 otherwise.

Constraint: every edge has at least one colored vertex#

This constraint ensures that, for every edge \((uv)\), either \(u\) or \(v\) or both are included in the vertex cover.

\[ \quad \sum_{(u,v) \in E} (1-x_u)(1-x_v) = 0. \]

Objective function: minimize the size of the vertex cover#

This can be interpreted for the bit population: $\( \quad \min \sum_v x_v. \)$

Modeling by JijModeling#

Next, we show how to implement the above equations using JijModeling. We first define the variables in the mathematical model described above. (Cf. graph partitioning problem.)

import jijmodeling as jm

# define variables
V = jm.Placeholder('V')
E = jm.Placeholder('E', ndim=2)
x = jm.BinaryVar('x', shape=(V,))
u = jm.Element('u', V)
e = jm.Element('e', E)

Constraint and objective function#

The constraint and the objective function are written as:

problem = jm.Problem('Vertex Cover')
problem += jm.Constraint('color', jm.sum(e, (1-x[e[0]])*(1-x[e[1]]))==0)
problem += x[:].sum()

On Jupyter Notebook, one can check the problem statement in a human-readable way by hitting.

problem
\[\begin{split}\begin{array}{cccc}\text{Problem:} & \text{Vertex Cover} & & \\& & \min \quad \displaystyle \sum_{\ast_{0} = 0}^{V - 1} x_{\ast_{0}} & \\\text{{s.t.}} & & & \\ & \text{color} & \displaystyle \sum_{e \in E} \left(- x_{e_{0}} + 1\right) \cdot \left(- x_{e_{1}} + 1\right) = 0 & \\\text{{where}} & & & \\& x & 1\text{-dim binary variable}\\\end{array}\end{split}\]

Prepare an instance#

We prepare a graph using Networkx.

import networkx as nx

# set the number of vertices
inst_V = 12
# create a random graph
inst_G = nx.gnp_random_graph(inst_V, 0.4)
# get information of edges
inst_E = [list(edge) for edge in inst_G.edges]
instance_data = {'V': inst_V, 'E': inst_E}

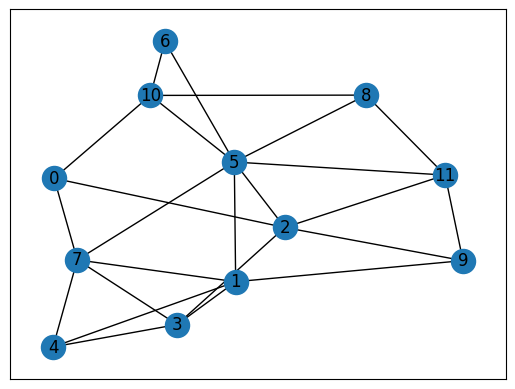
This graph is shown below.

import matplotlib.pyplot as plt

nx.draw_networkx(inst_G, with_labels=True)
plt.show()
../_images/6497ee55ff534953ebe6a1b104b1c4f0272fb58eba53bf3385163d0b413416fd.png

Solve by JijSolver#

We solve this problem using jijsolver.

import jijsolver

interpreter = jm.Interpreter(instance_data)
instance = interpreter.eval_problem(problem)
solution = jijsolver.solve(instance, time_limit_sec=1.0)

Visualize solution#

Finally, we visualize the solution obtained.

import matplotlib.pyplot as plt
import numpy as np

# get the indices of x == 1
df = solution.decision_variables
x_indices = np.ravel(df[df["value"]==1]["subscripts"].to_list())
# set color list for visualization
cmap = plt.get_cmap("tab10")
# initialize vertex color list
node_colors = [cmap(0)] * instance_data["V"]
# set vertex color list
for i in x_indices:
    node_colors[i] = cmap(1)
# draw the graph
nx.draw_networkx(inst_G, node_color=node_colors, with_labels=True)
plt.show()
../_images/6f31b656ad41f232e5fc2de25376d9234d635573798c0530c4907b7de4c12dfd.png

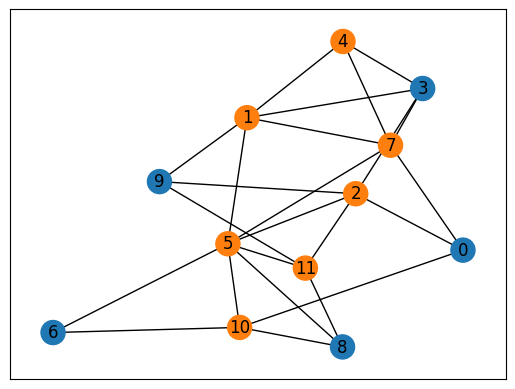
The above figure clearly shows a feasible vertex cover for the given graph.

Contents