Minimum Maximal Matching#
We show how to solve the minimum maximal matching problem using JijZeptSolver and JijModeling. This problem is also mentioned in 4.5. Minimal Maximal Matching on Lucas, 2014, “Ising formulations of many NP problems”.
What is Minimum Maximal Matching?#
The minimum maximal matching is a matching problem in graphs, where the matching is a set of edges in a graph that do not share any vertices with each other.
We assume that we have an undirected graph \(G = (V,E)\) and that \(C \subseteq E\) is a “coloring” of the edges. The constraints on \(C\) are given as follows. For each edge in \(C\), we color the two vertices it connects to the same. We then promise that no two edges in \(C\) share the same vertex and that \((u,v) \notin E\) if \(u, v \notin D\), where \(D\) is the set of vertices that are connected to any edge in \(C\). This is maximal in the sense that we cannot add any more edges to \(C\) without violating the first constraint while we must include all edges between uncolored vertices as long as they do not violate the first constraint; i.e. the empty set is not allowed. Such a coloring is the minimum when and only when the number of edges in \(C\) is the smallest possible.
Example#
For example, consider that we have a graph \(G = (V, E)\), where \(V = {1,2,3,4,5}\) and where \(E = {(1,2),(1,3),(2,3),(3,4),(4,5)}\). To find a maximal matching, we first have the empty set as a matching. Then, we add edges to the matching until we cannot add any more edges without violating the constraints. In such a small problem, one may be able to find the minimum maximal matching with some trial and error. Indeed, the minimum maximal matching for this graph is \(\{(1, 2), (3, 4)\}\), \(\{(1, 3), (4, 5)\}\), and \(\{(2, 3), (4, 5)\}\).
Mathematical model#
A binary variable \(x_e\) denotes whether or not the edge \(e\) is colored; The edge is colored if \(x_e\) is 1, and vice versa. We also introduce a binary variable \(y_v\) that denotes whether or not the vertex \(v\) is included in the matching (\(D\) in the above statements); the vertex is connected to a edge in \(C\) if \(y_v = 1\), and vice versa.
Constraint 1: relationship between \(x\) and \(y\)
By definition, the condition below obviously holds. $\( \quad y_v = \sum_{e \in E_v} x_e \quad \forall v, \)\( where \)E_v\( is the set of edges that are connected to the vertex \)v$.
Constraint 2: Every unselected edge is connected to at least one vertex connected to a selected edge
To formulate this, we use a basic observation: \(1-y_u\) is 0 if \(u\) is connected to a selected edge, and vice versa. Then, by counting \((1-y_{u})(1-y_{v})\) for all \((u,v) \in E\), we can check the violation of the constraint; i.e. if \((1-y_{u})(1-y_{v}) > 0\) for any \((u,v) \in E\), the edge \((u,v)\) can be selected without violating the constraints. $\( \quad \sum_{(u,v)\in E} (1-y_u)(1-y_v) = 0. \)$
Objective function: minimize the size of the matching
The size here means the number of edges selected. $\( \quad \min \sum_{e \in E} x_e. \)$
Modeling by JijModeling#
Next, we show how to implement the above equations using JijModeling. We first define the variables in the mathematical model described above.
import jijmodeling as jm
# define variables
V = jm.Placeholder('V')
E = jm.Placeholder('E', ndim=2)
num_E = E.shape[0]
x = jm.BinaryVar('x', shape=(num_E,))
y = jm.BinaryVar('y', shape=(V,))
v = jm.Element('v', V)
e = jm.Element('e', num_E)
Constraints and objective function#
The constraints and the objective function are written as:
problem = jm.Problem('Minimum Maximal Matching')
problem += jm.Constraint('y_x_relation', y[v] - jm.sum((e, (E[e][0]==v)|(E[e][1]==v)), x[e]) == 0 ,forall=v)
problem += jm.Constraint('unselected_edge', jm.sum(e, (1-y[E[e][0]])*(1-y[E[e][1]]))==0)
problem += x[:].sum()
On Jupyter Notebook, one can check the problem statement in a human-readable way by hitting.
problem
Prepare an instance#
Here we use the same instance with an example described above.
import networkx as nx
# set empty graph
inst_G = nx.Graph()
V = [0, 1, 2, 3, 4]
# add edges
inst_E = [[0, 1], [0, 2], [1, 2], [2, 3], [3, 4]]
inst_G.add_edges_from(inst_E)
# get the number of nodes
inst_V = list(inst_G.nodes)
num_V = len(inst_V)
instance_data = {'V': num_V, 'E': inst_E}
This graph is shown below.
import matplotlib.pyplot as plt
pos = nx.spring_layout(inst_G)
nx.draw_networkx(inst_G, pos=pos, with_labels=True)
plt.show()
Solve by JijZeptSolver#
We solve this problem using jijzept_solver.
import jijzept_solver
interpreter = jm.Interpreter(instance_data)
instance = interpreter.eval_problem(problem)
solution = jijzept_solver.solve(instance, time_limit_sec=1.0)
Visualize the solution#
The optimized solution can be seen as below.
import numpy as np
# get the indices of x == 1
df = solution.decision_variables_df
x_indices = np.ravel(df[(df["name"] == "x") & (df["value"] == 1.0)]["subscripts"].to_list())
# get the indices of y == 1
y_indices = np.ravel(df[(df["name"] == "y") & (df["value"] == 1.0)]["subscripts"].to_list())
# set color list for visualization
cmap = plt.get_cmap("tab10")
# set vertex color
vertex_colors = [cmap(1) if i in y_indices else cmap(0) for i in inst_V]
# set edge color list
edge_colors = ["red" if j in x_indices else "black" for j, _ in enumerate(instance_data["E"])]
# dwaw the figure with two subplots
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))
# plot the initial graph
nx.draw_networkx(inst_G, pos, with_labels=True, ax=ax1)
ax1.set_title('Initial Graph')
plt.axis('off')
ax1.set_frame_on(False) # Remove the frame from the first subplot
# plot the minimum maximal matching graph
nx.draw_networkx(inst_G, pos=pos, node_color=vertex_colors, edge_color=edge_colors, with_labels=True)
plt.axis('off')
ax2.set_title('Minimum Maximal Matching Graph')
# Show the plot
plt.show()
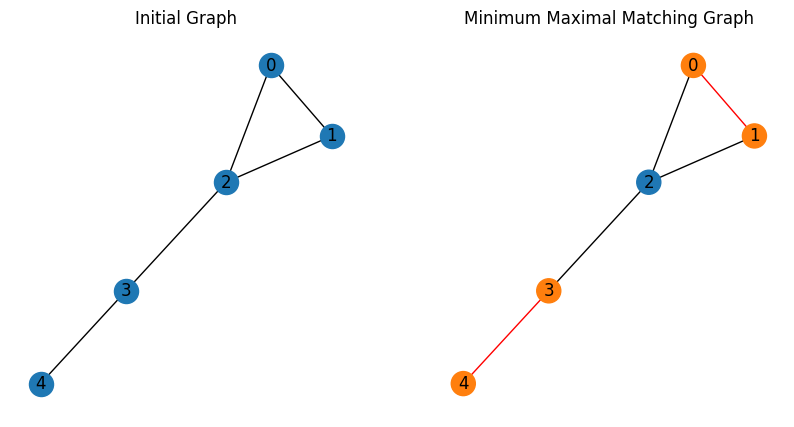
As expected, we have obtained the minimum maximal matching graph.
