グラフ分割問題

グラフ分割問題#

ここでは、JijSolverとJijModelingを用いて、グラフ分割問題を解く方法を説明します。 この問題は、Lucas, 2014, “Ising formulations of many NP problems” 2.2. Graph Partitioningでも触れられています。

グラフ分割問題とは#

グラフ分割問題は、グラフを2つの頂点数が等しい部分グラフに分割するとき、それらの部分グラフ間を結ぶ辺の数を最小にすることを考える問題です。

例#

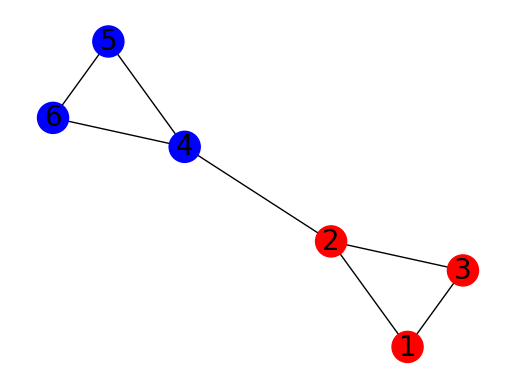
次のような問題を考えましょう。 1~6の番号を持つ6つの頂点グラフにおいて

  • 1は2, 3につながる

  • 2は1, 3, 4につながる

  • 3は1, 2につながる

  • 4は2, 5, 6につながる

  • 5は4, 6につながる

  • 6は4, 5につながる

辺を持つとします。 それらの辺の数の差が最小となるように、3つの頂点をもつ2つの部分グラフに分割することを考えましょう。 この場合、最適解は\(\{1, 2, 3\}, \{4, 5, 6\}\)のようになり、2つの部分グラフが(2, 4)の1つの辺だけで結ばれているようなものとなります。

数理モデル#

無向グラフを\(G = (V, E)\)としましょう。 ここで\(V\)はグラフ頂点の集合、\(E\)はグラフの辺の集合を表します。 このグラフを\(V_1, V_2\)に分割するとき、それらの部分グラフの間を結ぶ辺の数を最小にするのが目標です。 そこで、頂点\(u\)が部分グラフ\(V_1\)に属するとき1, \(V_2\)に属するとき0となるようなバイナリ変数\(x_u\)を導入します。

制約: 頂点集合は、等しい頂点数の2つの部分グラフに分割しなければならない

これは、次のような数式で表現されます。

\[ \sum_{u \in V} x_u = \frac{V}{2} \tag{1} \]

目的関数: 分割されたグラフ間の辺の数を最小化する

\[ \min \quad \sum_{(uv) \in E} (\{x_{u} (1-x_{v})\}+\{(1-x_{u}) x_{v}\}) \tag{2} \]

第一項の\(x_u (1-x_v)\)は、辺\((u, v)\)が\(V_1\)と\(V_2\)の境界にある場合 (例えば\(u\)は\(V_1\)に属し\(v\)は\(V_2\)に属する場合)のみ1となり、それ以外の場合には0となります。 同様に、第二項の\((1-x_u) x_v\)は、辺\((u, v)\)が\(V_2\)と\(V_1\)の境界にある場合 (例えば\(u\)は\(V_2\)に属し\(v\)は\(V_1\)に属する場合)のみ1となり、それ以外の場合には0となります。したがってこの目的関数が、グラフ分割がどれだけ達成されたかの指標となることがわかります。

JijModelingによるモデル化#

次に、JijModelingを用いた実装を示します。最初に、上述の数理モデルで用いる変数を定義しましょう。

import jijmodeling as jm

# define variables
V = jm.Placeholder('V')
E = jm.Placeholder('E', ndim=2)
x = jm.BinaryVar('x', shape=(V,))
u = jm.Element('u', belong_to=V)
e = jm.Element('e', belong_to=E)

V=jm.Placeholder("V")はグラフの頂点数を表します。 E=jm.Placeholder("E", ndim=2)はグラフの辺集合を意味します。 そしてx=jm.BinaryVar("x", shape=(V, ))でバイナリ変数のリストを準備し、数理モデルで用いる添字をuとして定義しています。 最後に、eは辺を表す変数であり、e[0], e[1]は辺で結ばれる2つの頂点を表しています。

制約#

式(1)の制約を実装しましょう。

# set problem
problem = jm.Problem('Graph Partitioning')
# set constraint: the vertices must be partitioined into two equal-sized sets
const = jm.sum(u, x[u])
problem += jm.Constraint('constraint', const==V/2)

目的関数#

次は、式(2)の目的関数の実装です。

# set objective function: minimize the number of edges crossing the partition
A_1 = x[e[0]]*(1-x[e[1]])
A_2 = (1-x[e[0]])*x[e[1]]
problem += jm.sum(e, (A_1 + A_2))

実装した数理モデルを、Jupyter Notebook上で表示してみましょう。

problem
\[\begin{split}\begin{array}{cccc}\text{Problem:} & \text{Graph Partitioning} & & \\& & \min \quad \displaystyle \sum_{e \in E} \left(x_{e_{0}} \cdot \left(- x_{e_{1}} + 1\right) + \left(- x_{e_{0}} + 1\right) \cdot x_{e_{1}}\right) & \\\text{{s.t.}} & & & \\ & \text{constraint} & \displaystyle \sum_{u = 0}^{V - 1} x_{u} = V \cdot 2^{(-1)} & \\\text{{where}} & & & \\& x & 1\text{-dim binary variable}\\\end{array}\end{split}\]

インスタンスの準備#

NetworkXを用いて、グラフを準備しましょう。 ここでは、12個の頂点をもつランダムグラフを生成してみます。

import networkx as nx

# set the number of vertices
inst_V = 12
# create a random graph
inst_G = nx.gnp_random_graph(inst_V, 0.4)
# get information of edges
inst_E = [list(edge) for edge in inst_G.edges]
instance_data = {'V': inst_V, 'E': inst_E}

JijSolverで解く#

jijsolverを用いて、この問題を解いてみましょう。

Solve by JijSolver#

We solve this problem using jijsolver.

import jijsolver

interpreter = jm.Interpreter(instance_data)
instance = interpreter.eval_problem(problem)
solution = jijsolver.solve(instance, time_limit_sec=1.0)

解の可視化#

最後に、得られた解を可視化してみましょう。

import matplotlib.pyplot as plt
import numpy as np

df = solution.decision_variables
x_indices = np.ravel(df[df["value"]==1]["subscripts"].to_list())
# set color list for visualization
cmap = plt.get_cmap("tab10")
# initialize vertex color list
node_colors = [cmap(0)] * instance_data["V"]
# set vertex color list
for i in x_indices:
    node_colors[i] = cmap(1)
# make figure
nx.draw_networkx(inst_G, node_color=node_colors, with_labels=True)
plt.show()
../_images/b7d32738879d7b09e3ceb46b8bc3da44c82b73072e4e63a0c0e841fc29e54e41.png

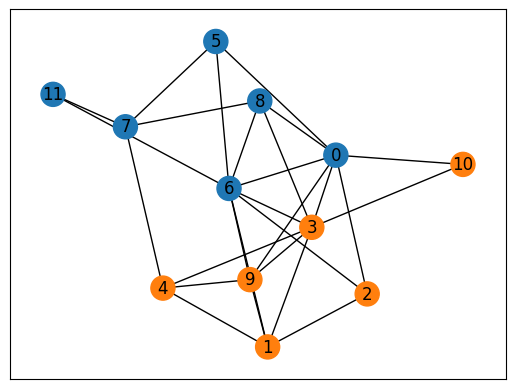
可視化結果から、このグラフ分割問題の実行可能解が得られていることがわかります。

Contents