クリーク問題#
ここでは、JijZeptSolverとJijModelingを用いて、クリーク問題を解く方法を説明します。 この問題は、Lucas, 2014, “Ising formulations of many NP problems”の2.3. Cliqueでも触れられています。
クリーク問題とは#
この問題は、与えられたグラフ中にサイズ\(K\)のクリーク (完全グラフ) があるかどうかを判定する問題です。
完全グラフ#
完全グラフとは、全ての頂点がお互いに辺で結ばれているようなグラフのことです (ただし、ループや多重辺は含みません。) 完全グラフの例を以下に示します。
上述のように、完全グラフの頂点は、他の全ての頂点と接続しています。 よって完全無向グラフ \(G = (V, E)\)は、頂点集合\(V\)から2つを選び出す組合せの数 \({}_V C_2 = \frac{1}{2} V (V-1)\)個の辺を持ちます。
数理モデル#
最初に、頂点\(v\)が部分グラフに含まれるとき1、そうでないとき0となるようなバイナリ変数\(x_v\)を導入しましょう。
制約 1: \(x_v\)の総和が\(K\)に一致しなければならない#
この問題では、頂点\(v\)が部分グラフの一部のとき\(x_v = 1\)となることから、この制約は次のようになります。
制約 2: 部分グラフは完全グラフでなければならない#
辺集合\(E\)の中でも、\(E_W\)は頂点集合\(W\)どうしを結ぶ辺集合で、そのようにしてできる部分グラフを\(G(W, E_W)\)としましょう。 これが完全グラフの場合、この部分グラフは先ほどの議論から\(\frac{1}{2} W (W-1)\)の辺を持つことになります。 先ほどのバイナリ変数を用いると、この部分グラフの辺数は\(\sum_{(uv) \in E_W} x_u x_v\)のように書けることから、この制約は次のようになります。
JijModelingによるモデル化#
次に、JijModelingを用いた実装を示します。 最初に、上述の数理モデルで用いる変数を定義します。
import jijmodeling as jm
# define variables
V = jm.Placeholder('V')
E = jm.Placeholder('E', ndim=2)
K = jm.Placeholder('K')
x = jm.BinaryVar('x', shape=(V,))
u = jm.Element('u', (V))
e = jm.Element('e', E)
ここで定義したものは、グラフ分割問題の変数に、\(K\)を加えたものです。
制約 1#
式(1)の制約を実装しましょう。
# set problem
problem = jm.Problem('Clique')
# set constraint: sum of $x_v$ must equal K
problem += jm.Constraint('constraint1', jm.sum(u, x[u])==K)
制約 2#
次に、式(2)の制約を実装します。
# set constraint: the subgraph must be complete
problem += jm.Constraint('constraint2', jm.sum(e, x[e[0]]*x[e[1]])==1/2*K*(K-1))
実装した数理モデルを、Jupyter Notebookで表示しましょう。
problem
インスタンスの準備#
Networkxを用いて、グラフを準備しましょう。 ここでは\(K=4\)の完全部分グラフを持つようなグラフを生成します。
import networkx as nx
# set the number of random vertices
inst_V1 = 3
# create a random graph
inst_G1 = nx.gnp_random_graph(inst_V1, 0.2)
# set the size K
inst_K = 4
# create a complete graph with K vertices
inst_G2 = nx.complete_graph(inst_K)
# set the number of vertices
inst_V = inst_V1 + inst_K
# add the complete graph to the given graph
inst_G = nx.union(inst_G1, inst_G2, rename=('G-', 'K-'))
# connect each vertex of G1 to vertex 0 of G2
for i in range(inst_V1):
inst_G.add_edge(f'G-{i}', 'K-0')
# relabel the nodes using normal numbers from 0
mapping = {node: i for i, node in enumerate(inst_G.nodes)}
inst_G = nx.relabel_nodes(inst_G, mapping)
# get information of edges
inst_E = [list(edge) for edge in inst_G.edges]
instance_data = {'V': inst_V, 'E': inst_E, 'K': inst_K}
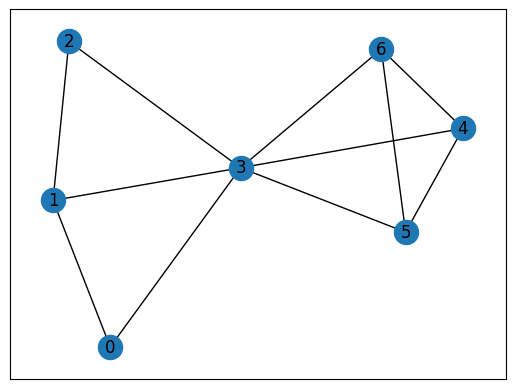
クリーク問題で用いるグラフを、以下に描画してみましょう。
import matplotlib.pyplot as plt
pos = nx.spring_layout(inst_G)
nx.draw_networkx(inst_G, pos, with_labels=True)
plt.show()
JijZeptSolverで解く#
この問題を、jijzept_solverを用いて解きましょう。
import jijzept_solver
interpreter = jm.Interpreter(instance_data)
instance = interpreter.eval_problem(problem)
solution = jijzept_solver.solve(instance, time_limit_sec=1.0)
解の可視化#
得られた解を可視化してみましょう。
import numpy as np
df = solution.decision_variables_df
vertices = np.ravel(df[df["value"]==1]["subscripts"].to_list())
print(vertices)
# set color list for visualization
cmap = plt.get_cmap("tab10")
# initialize vertex color list
node_colors = [cmap(0)] * instance_data["V"]
# set the vertex color list
for i in vertices:
node_colors[i] = cmap(1)
# highlight the edge of clique
highlight_edges = [(u, v) for (u, v) in inst_G.edges() if u in vertices and v in vertices]
# make figure
nx.draw_networkx(inst_G, pos, node_color=node_colors, with_labels=True)
nx.draw_networkx_edges(inst_G, pos, edgelist=highlight_edges, edge_color='red')
plt.show()
[3 4 5 6]
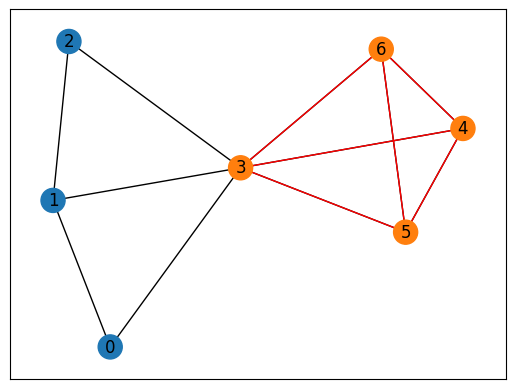
上図のように、制約が満たされた解が得られました。
最後に、\(N\)個の値を取り得る変数を符号化するのに必要なスピン数を、削減する手法を紹介しましょう。 整数\(M\)を定義し、\(2^M \leq N < 2^{(M+1)}\)とすることで、\(N\)個のバイナリ変数の代わりに\(M+1\)個のバイナリ変数を使うことができます。 これはクリーク問題のNP困難バージョンを解くのに使うことができます。 これにより必要なスピン数を、\(N +1+\lfloor \log \Delta \rfloor\)に減らすことができます。 ここで\(\Delta\)は、クリーク問題で考えられているグラフの最大次数を表します。 この手法はLucas, 2014, “Ising formulations of many NP problems” 2.4. Reducing \(N\) to \(\log N\) Spins in Some Constraints でも触れられています。
