頂点被覆問題

頂点被覆問題#

ここではJijSolverとJijModelingを用いて、頂点被覆問題を解く方法を説明します。 この問題は、Lucas, 2014, “Ising formulations of many NP problems” 4.3. Vertex Coverでも触れられています。

頂点被覆問題とは#

頂点被覆問題は次のように定義されます。 無向グラフ \(G=(V, E)\)が与えられたとき、全ての辺が両端に異なる色の頂点を持つように色をつけるとき、最小数の色付け頂点数となるように頂点を決める問題です。 言い換えれば、グラフにおける全ての辺を被覆するような頂点の最小集合を求める問題と言えます。

例題として、次のような無向グラフを考えましょう。

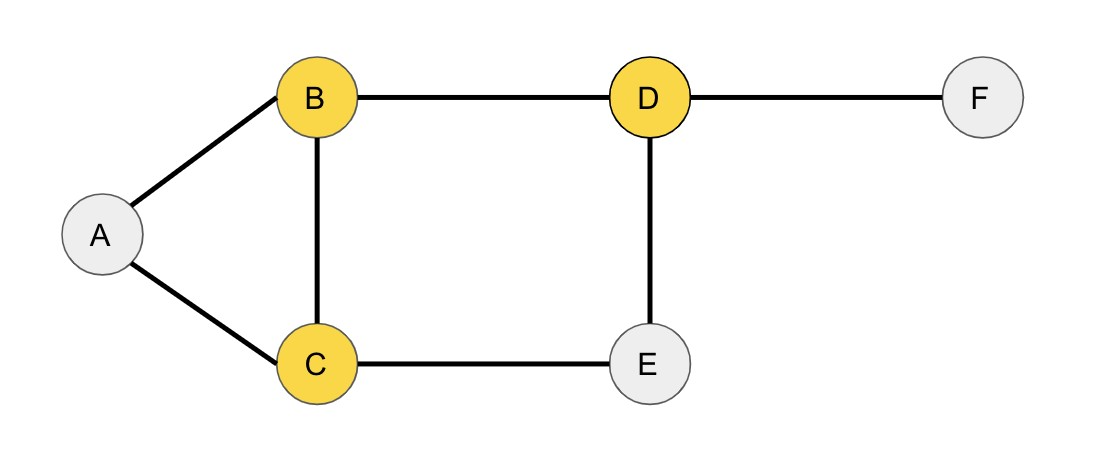
このグラフの頂点をA, B, C, D, E, Fとし、頂点どうしを結ぶ線分は辺として表現されています。 このグラフにおける頂点被覆は、\(\{B, C, D\}\)となります。 各辺は少なくとも1つ、これらの頂点を含んでいます。

  • 辺(A, B)は頂点Bを被覆されている

  • 辺(A, C)は頂点Cを被覆されている

  • 辺(B, C)は頂点B, Cを被覆されている

  • 辺(B, D)は頂点B, Dを被覆されている

  • 辺(C, E)は頂点Cを被覆されている

  • 辺(D, E)は頂点Dを被覆されている

  • 辺(D, F)は頂点Dを被覆されている

数理モデル#

まず、頂点\(v\)が色付けされたとき1、そうでないとき0となるようなバイナリ変数\(x_v\)を導入します。

制約: 各辺は少なくとも1つの色付けされた頂点を持つ#

各辺\((uv)\)において、頂点\(u\)または頂点\(v\)、あるいは両方の頂点を被覆する必要があります。

\[ \quad \sum_{(u,v) \in E} (1-x_u)(1-x_v) = 0. \]

目的関数: 頂点被覆の数を最小化する#

これは次のように解釈することができます。

\[ \quad \min \sum_v x_v. \]

JijModelingによるモデル化#

次に、JijModelingを用いて上述の数式を実装してみましょう。 最初に、数理モデルを記述するのに必要な変数を定義しましょう。 (グラフ分割問題を参照)

import jijmodeling as jm

# define variables
V = jm.Placeholder('V')
E = jm.Placeholder('E', ndim=2)
x = jm.BinaryVar('x', shape=(V,))
u = jm.Element('u', V)
e = jm.Element('e', E)

制約と目的関数#

制約と目的関数を、次のように実装しましょう。

problem = jm.Problem('Vertex Cover')
problem += jm.Constraint('color', jm.sum(e, (1-x[e[0]])*(1-x[e[1]]))==0)

problem += x[:].sum()

Jupyter Notebook上で次のようにn湯力することで、実装された数式を確認することができます。

problem
\[\begin{split}\begin{array}{cccc}\text{Problem:} & \text{Vertex Cover} & & \\& & \min \quad \displaystyle \sum_{\ast_{0} = 0}^{V - 1} x_{\ast_{0}} & \\\text{{s.t.}} & & & \\ & \text{color} & \displaystyle \sum_{e \in E} \left(- x_{e_{0}} + 1\right) \cdot \left(- x_{e_{1}} + 1\right) = 0 & \\\text{{where}} & & & \\& x & 1\text{-dim binary variable}\\\end{array}\end{split}\]

インスタンスの準備#

Networkxを用いてグラフを準備しましょう。

import networkx as nx

# set the number of vertices
inst_V = 12
# create a random graph
inst_G = nx.gnp_random_graph(inst_V, 0.4)
# get information of edges
inst_E = [list(edge) for edge in inst_G.edges]
instance_data = {'V': inst_V, 'E': inst_E}

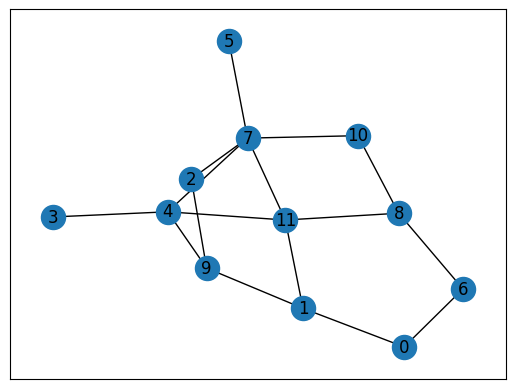
このグラフを可視化すると、次のようになります。

import matplotlib.pyplot as plt

nx.draw_networkx(inst_G, with_labels=True)
plt.show()
../_images/a2fcd243c72b71be8e1570645c8015514800d8915b400660693fe865ff754069.png

JijSolverで解く#

jijsolverを用いて、この問題を解きましょう。

import jijsolver

interpreter = jm.Interpreter(instance_data)
instance = interpreter.eval_problem(problem)
solution = jijsolver.solve(instance, time_limit_sec=1.0)

解の可視化#

最後に、得られた解を可視化してみましょう。

import matplotlib.pyplot as plt
import numpy as np

# get the indices of x == 1
df = solution.decision_variables
x_indices = np.ravel(df[df["value"]==1]["subscripts"].to_list())
# set color list for visualization
cmap = plt.get_cmap("tab10")
# initialize vertex color list
node_colors = [cmap(0)] * instance_data["V"]
# set vertex color list
for i in x_indices:
    node_colors[i] = cmap(1)
# draw the graph
nx.draw_networkx(inst_G, node_color=node_colors, with_labels=True)
plt.show()
../_images/50d79798286507df80de071ebc12771e7f302ec219f545714bb025a526b88e80.png

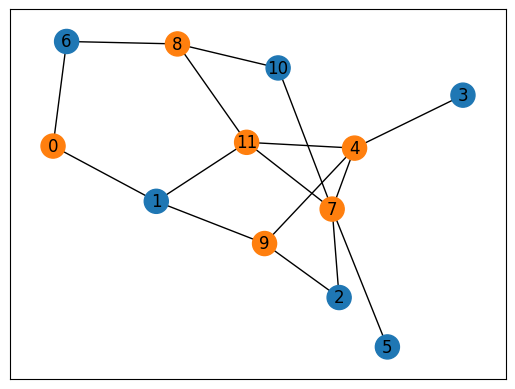
上図からわかるように、制約の満たされている実行可能解の頂点被覆を示すことができました。

Contents