ディープ・スペース・ネットワークのスケジューリング問題

ディープ・スペース・ネットワークのスケジューリング問題#

ディープ・スペース・ネットワーク（以下、DSN）とは、NASAが保有する電波望遠鏡のネットワークです。DSNは惑星観測だけでなく、宇宙探査機との通信にも利用されています。宇宙探査機の数が増加する中、通信のスケジューリングは非常に難しい問題となっています。本チュートリアルでは、D-Waveが定式化したDSNのスケジューリング問題をどのように解くかを説明します。

導入#

DSNは、オーストラリア・スペイン・アメリカにまたがる電波望遠鏡を繋いだネットワークです。これらあの電波望遠鏡は主に、宇宙に打ち上げられた宇宙探査機との交信、電波波長帯域での惑星観測ミッションに役立てられています。しかし、宇宙探査機の増加やその交信の複雑化が進む昨今では、どのアンテナをどの宇宙探査機との交信に用いるか（あるいは、どのミッションに割り当てるか）のスケジューリングは困難を極めます。近年では、複数台の電波望遠鏡をネットワークで繋ぎ、これらをあるパターンに従って操作することで信号間の干渉を利用する電波干渉技術も注目を集めており、今後もスケジューリングの困難さは増していくでしょう。

Guillaume et al., 2022では、このスケジューリング問題をQUBO定式化し、D-Waveのハイブリッドソルバーを用いて解きました。今回はその定式化をJijModelingで実装し、解いてみることとします。

定式化#

\(N\) 個のリクエストがあり、これを \(\mathcal{Q} = \{Q_1, Q_2, \dots, Q_N\}\) とします。あるリクエスト \(Q_n\) が \(M\) 個の(アンテナや装置などの地上の)リソースに割り当てることを考えます。このリソースの集合を \(\mathcal{S} = \{S_1, S_2, \dots, S_M\}\) とするとき、各地上のリソース \(S_m\) に対し、宇宙にある衛星が見える期間を \(\mathcal{V} = \{V_1, V_2, \dots, V_K\}\) とします。衛星が見える期間の開始時刻(rise time)と終了時刻(set time)をそれぞれrt, stと定義します。また、実際に衛星に信号を送信が開始できるようになるのはrtからわずかに遅れた時刻であり、送信ができるのはstからわずかに早い時刻までであるため、実際に送信が開始できる時刻と送信が終了する時刻をtn, tfと定義することとします。加えて、各リクエストに対して、要求された装置を準備する時間、装置を撤去するための時間が必要なので、それらをsu, tdと定義します。さらに、各リクエストにはトラッキングの継続時間drが定められていることとします。

これらをインスタンスデータとして、最適化を行います。DSNスケジュール最適化の目的は、全てのリクエストを満たすこと、言い換えればリクエストごとに正確に一つのアクションをスケジュールすることです。そのために、 \(x_{n, m, k, t}\) のようなバイナリ変数を用意しましょう。これは時刻 \(t\) からトラッキングを開始し、衛星が見える期間 \(k\) の間にリソース \(m\) を用いてリクエスト \(n\) を処理する場合に1、そうでない場合に0となるようなものです。

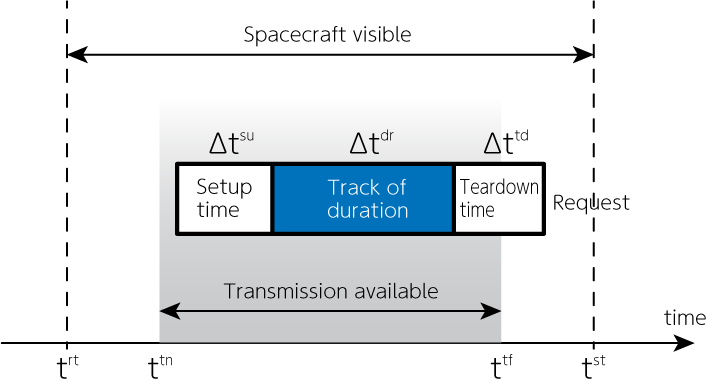
制約1: 全てのリクエストは決められた時間内に、どれかのアンテナで処理されなければならない#

制約1を数式で表現すると、以下のようになります。

\[ \sum_{m=1}^M \sum_{k=1}^K \sum_{t} x_{n, m, k, t} = 1 \qquad \forall n, t^\mathrm{tn} \leq t \leq t^\mathrm{tf}-\Delta t^\mathrm{dr} \tag{1} \]

実際にリクエスト送信を開始できるtnから、tf-drまでにリクエストの送信を終える必要があります。drだけトラッキング継続時間がかかるため、その分早くリクエストを送信しておかなければなりません。

制約2: 衝突が起きてはならない#

次の図に示すように、同じアンテナで同じ時間に2つのスケジュールが重なってはなりません。

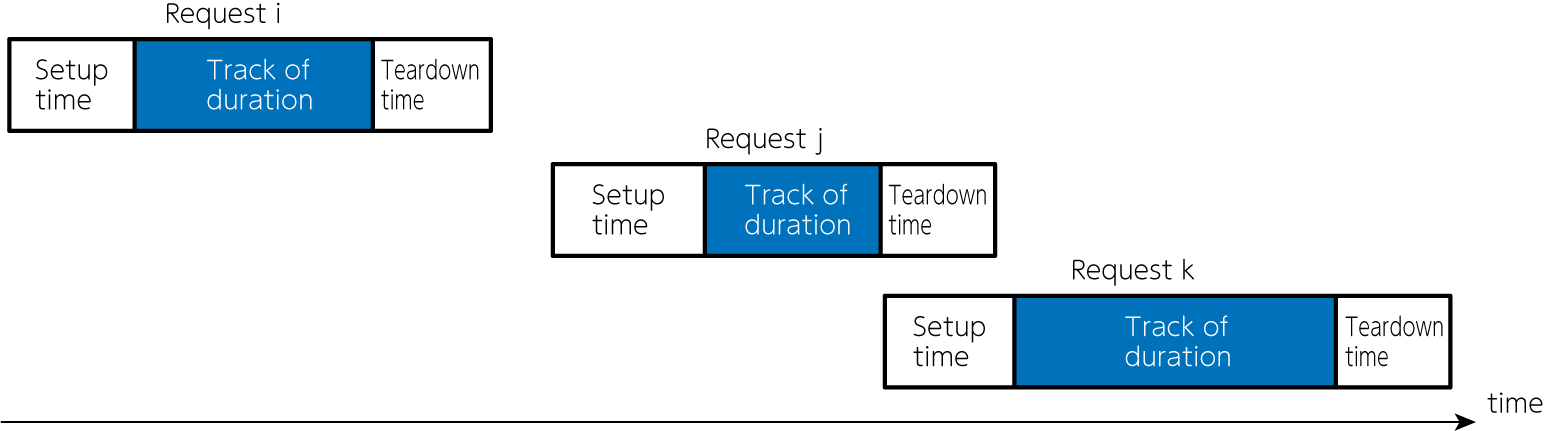
上の図では、リクエスト \(i\) と \(j\)、 \(j\) と \(k\) は重なっていませんが、 \(j\) と \(k\) が重なってしまっています。このようなスケジュールの重なりは避けねばなりません。これを数式で表現すると以下のようになります。

\[\begin{split} \begin{align} & x_{n, m, k, t} x_{n', m', k', t'} = 0 \\ & \quad (Q_n \neq Q_{n'}, S_m = S_{m'}, t-\Delta t^\mathrm{su} \leq t'-\Delta t^\mathrm{su'} \leq t + \Delta t^\mathrm{dr} + \Delta t^\mathrm{td} \ \mathrm{or} \ t' - \Delta t^\mathrm{su'} \leq t-\Delta t^\mathrm{su} \leq t' + \Delta t^\mathrm{dr'} + \Delta t^\mathrm{td'}) \end{align} \tag{2} \end{split}\]

JijModelingによる定式化#

以下では、JijModelingを用いて上記で定式化した数理モデルを実装します。

パラメーターと決定変数#

式(1)および式(2)を定義するために必要なパラメーターと決定変数を定義しましょう。

import jijmodeling as jm

AT = jm.Placeholder("AT", ndim=4)
max_AT = jm.Placeholder("max_AT")
N = jm.Placeholder("N")
M = jm.Placeholder("M")
K = jm.Placeholder("K")
su = jm.Placeholder("su", ndim=1)
dr = jm.Placeholder("dr", ndim=1)
td = jm.Placeholder("td", ndim=1)
x = jm.BinaryVar("x", shape=(N, M, K, max_AT))
n1 = jm.Element("n1", belong_to=N)
n2 = jm.Element("n2", belong_to=N)
m = jm.Element("m", belong_to=M)
k1 = jm.Element("k1", belong_to=K)
k2 = jm.Element("k2", belong_to=K)
t1 = jm.Element("t1", belong_to=AT[n1, m, k1])
t2 = jm.Element("t2", belong_to=AT[n2, m, k2])

AT はリクエストの処理開始時間、 max_AT は AT の最大値、 N はリクエストの総数、 M は地上のリソースの数、 K は宇宙にある衛星の見える期間の総数として定義しています。 su, dr, td はそれぞれ装置の準備時間、トラッキングの継続時間、装置の撤去時間を定義しています。そして、決定変数 \(x_{n, m, k, t}\) として x を定義しており、後の数理モデルの実装のために必要な添字として n1, n2, m, k1, k2, t1, t2 を定義しています。ここで t1, t2 の取り得る範囲を AT[n1, m, k1], AT[n2, m, k2] としていることにも注意してください。これは数理モデルの \(t_1 \in \mathrm{AT}_{n1, m, k1}, t_2 \in \mathrm{AT}_{n2, m, k2}\) の部分を表現しています。

数理モデルの定義#

次に、式(1)および式(2)を制約とする数理モデルを実装します。

problem = jm.Problem("Radio_telescope_scheduling")
problem += jm.Constraint("onehot", jm.sum([m, k1, t1], x[n1, m, k1, t1])==1, forall=n1)
problem += jm.Constraint(
    "conflict",
    x[n1, m, k1, t1]*x[n2, m, k2, t2]==0, 
    forall=[
        n1, (n2, n2!=n1), m, k1, k2, t1, 
        (t2, (t1-su[n1]<=t2-su[n2]) & (t2-su[n2]<=t1+dr[n1]+td[n1]) | ((t2-su[n2]<=t1-su[n1]) & (t1-su[n1]<=t2+dr[n2]+td[n2])))
    ],
)

JijModelingでは、式(1)に含まれる \(\sum_{m, k, t}\) を sum([m, k, t], ...) のように定義することができます。また、式(2)に含まれる複雑な条件式も、上記のコードのように実装することができます。

これで数理モデルの実装は完了です。正しく数理モデルが実装されているかをLaTeX表示を通して確認してみましょう。

problem
\[\begin{split}\begin{array}{cccc}\text{Problem:} & \text{Radio\_telescope\_scheduling} & & \\& & \min \quad \displaystyle 0 & \\\text{{s.t.}} & & & \\ & \text{conflict} & \displaystyle x_{n1, m, k1, t1} \cdot x_{n2, m, k2, t2} = 0 & \forall n1 \in \left\{0,\ldots,N - 1\right\} \forall n2 \in \left\{n2 \in \left\{0,\ldots,N - 1\right\} \mid n2 \neq n1 \right\} \forall m \in \left\{0,\ldots,M - 1\right\} \forall k1 \in \left\{0,\ldots,K - 1\right\} \forall k2 \in \left\{0,\ldots,K - 1\right\} \forall t1 \in AT_{n1, m, k1} \forall t2 \in \left\{t2 \in AT_{n2, m, k2} \mid t1 - su_{n1} \leq t2 - su_{n2} \land t2 - su_{n2} \leq t1 + dr_{n1} + td_{n1} \lor t2 - su_{n2} \leq t1 - su_{n1} \land t1 - su_{n1} \leq t2 + dr_{n2} + td_{n2} \right\} \\ & \text{onehot} & \displaystyle \sum_{m = 0}^{M - 1} \sum_{k1 = 0}^{K - 1} \sum_{t1 \in AT_{n1, m, k1}} x_{n1, m, k1, t1} = 1 & \forall n1 \in \left\{0,\ldots,N - 1\right\} \\\text{{where}} & & & \\& x & 4\text{-dim binary variable}\\\end{array}\end{split}\]

インスタンスデータの準備#

数理モデルの実装が完了したので、パラメーターに入力する値としてインスタンスデータを準備しましょう。今回の説明では以下のコードから生成されるインスタンスデータを利用します。

import collections
import numpy as np

def flatten(l):
    for el in l:
        if isinstance(el, collections.abc.Iterable) and not isinstance(el, (str, bytes)):
            yield from flatten(el)
        else:
            yield el

# set the number of requests
inst_N = 12
# set a list of set up time period: su
rng = np.random.default_rng(1234)
inst_su = rng.normal(2.0, 0.5, inst_N).tolist()
# set a list of track duration: dr
inst_dr = rng.normal(2.0, 0.5, inst_N).tolist()
# set a list of tear down time period: td
inst_td = rng.normal(1.5, 0.5, inst_N).tolist()
# set a array of transmission-on time: tn
inst_tn = np.array([[0, 6, 12, 18], [2, 8, 14, 20], [4, 10, 16, 22]])
# set a array of transmission-off time: tf
inst_tf = np.array([[4, 10, 16, 22], [6, 12, 18, 24], [8, 14, 20, 26]])
# get the number of resources and viewperiods
inst_M = inst_tn.shape[0]
inst_K = inst_tn.shape[1]
# compute a array of available time tn ≤ t ≤ tf - dr
inst_available = []
for n in range(inst_N):
    inst_available.append([])
    for i in range(inst_M):
        inst_available[n].append([])
        for j in range(inst_tf.shape[1]):
            inst_available[n][i].append(list(range(inst_tn[i, j], np.floor(inst_tf[i, j]-inst_dr[n]).astype(int))))
# compute max(available time)
inst_max_available = np.amax(list(flatten(inst_available))) + 1
instance_data = {"AT": inst_available, "su": inst_su, "dr": inst_dr, "td": inst_td, "max_AT": inst_max_available, "N": inst_N, "M": inst_M, "K": inst_K}

DSNのスケジューリング問題を解く#

さて、これでDSNのスケジューリング問題を解くためのすべての準備が完了しました。以下のコードを実行してDSNのスケジューリング問題を解いてみましょう。以下のコードは ommx-pyscipopt-adapter を介して最適化ソルバー SCIP で問題を解くものです。

from ommx_pyscipopt_adapter import OMMXPySCIPOptAdapter

interpreter = jm.Interpreter(instance_data)
ommx_instance = interpreter.eval_problem(problem)

ommx_solution = OMMXPySCIPOptAdapter.solve(ommx_instance)
df = ommx_solution.decision_variables
df[df["value"] == 1.0]
kind lower upper name subscripts description substituted_value value
id
0 binary 0.0 1.0 x [0, 0, 0, 0] <NA> <NA> 1.0
504 binary 0.0 1.0 x [1, 2, 0, 4] <NA> <NA> 1.0
631 binary 0.0 1.0 x [2, 0, 1, 6] <NA> <NA> 1.0
1096 binary 0.0 1.0 x [3, 1, 3, 21] <NA> <NA> 1.0
1262 binary 0.0 1.0 x [4, 0, 2, 12] <NA> <NA> 1.0
1602 binary 0.0 1.0 x [5, 1, 0, 2] <NA> <NA> 1.0
1893 binary 0.0 1.0 x [6, 0, 3, 18] <NA> <NA> 1.0
2264 binary 0.0 1.0 x [7, 1, 2, 14] <NA> <NA> 1.0
2533 binary 0.0 1.0 x [8, 1, 1, 8] <NA> <NA> 1.0
2966 binary 0.0 1.0 x [9, 2, 2, 16] <NA> <NA> 1.0
3235 binary 0.0 1.0 x [10, 2, 1, 10] <NA> <NA> 1.0
3597 binary 0.0 1.0 x [11, 2, 3, 22] <NA> <NA> 1.0

解の可視化#

最後に、上記で得られた解を用いて実行可能なスケジュールを確認してみましょう。以下のコードでスケジュールを可視化することができます。

import matplotlib.pyplot as plt
import matplotlib.ticker as ticker

subscripts = df[df["value"] == 1.0]["subscripts"].to_list()
n_indices = [subscript[0] for subscript in subscripts]
m_indices = [subscript[1] for subscript in subscripts]
k_indices = [subscript[2] for subscript in subscripts]
t_indices = [subscript[3] for subscript in subscripts]
# make plot
fig, ax = plt.subplots()
# set x- and y-axis
ax.set_xlabel("Time")
ax.set_yticks(range(inst_M))
ax.set_yticklabels(["Resource {}".format(m) for m in range(inst_M)])
ax.get_xaxis().set_major_locator(ticker.MaxNLocator(integer=True))
# make bar plot for transmission using broken_barh
for n, m, k, t in zip(n_indices, m_indices, k_indices, t_indices):
    ax.broken_barh([(t, inst_dr[n])], (m-0.5, 1), color="dodgerblue")
    ax.broken_barh([(t-inst_su[n], inst_su[n])], (m-0.5, 1), color="gold")
    ax.broken_barh([(t+inst_dr[n], inst_td[n])], (m-0.5, 1), color="violet")
# make bar plot for available time
for m, (list_tn, list_tf) in enumerate(zip(inst_tn, inst_tf)):
    for tn, tf in zip(list_tn, list_tf):
        ax.broken_barh([(tn, tf-tn-1)], (m-0.5, 1), color="lightgray", alpha=0.4)
# make legend
ax.scatter([], [], color="lightgray", label="Transimission available", marker="s")
ax.scatter([], (), color="dodgerblue", label="Tracking", marker="s")
ax.scatter([], (), color="gold", label="Set up", marker="s")
ax.scatter([], (), color="violet", label="Tear down", marker="s")
ax.legend(bbox_to_anchor=(1.45, 1.0))
# show plot
plt.show()
../_images/8b0cbea6a28dd5862543eef36af789bbebd8026b45803f62b4eb7f1d6b1eccba.png

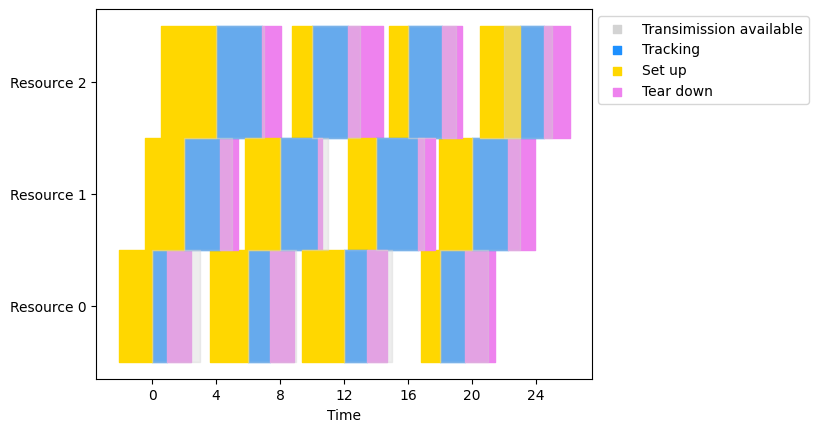
上の図では、灰色が各リソースと宇宙探査機が通信できる時間を示しており、青色がトラッキング時間、黄色とマゼンタが各リクエストの準備時間と撤去時間を示しています。灰色（通信時間）が青色（トラッキング時間）にすべて塗りつぶされているため、このスケジュールであればすべての通信を実現できることがわかります。

参考文献#

Contents