最小極大マッチング問題

ここではJijSolverとJijModelingを用いて、最小極大マッチング問題を解く方法を紹介します。 この問題は、Lucas, 2014, “Ising formulations of many NP problems” 4.5. Minimal Maximal Matchingでも触れられています。

最小極大マッチング問題とは

最小極大マッチング問題は、グラフにおけるマッチング問題の一つです。 グラフ中の辺の中で、他のどの辺とも頂点を共有しないような辺集合を探す問題となります。
無向グラフを\(G=(V, E)\)とし、辺の中で色付けされたものを\(C \subseteq E\)のように書くことにしましょう。 \(C\)に対する制約は次のようになります。 集合\(C\)の各辺に対し、その辺で結ばれる2つの頂点を同じ色に塗ります。 そして\(C\)に含まれるどの2つの辺も、同じ色の頂点を共有してはなりません。 すなわち、\(C\)の辺が結ぶ頂点の集合を\(D\)のように書くと、\(u, v \in D\)ならば\((u, v)\notin E\)でなければなりません。 1つ目の制約を破ることなく\(C\)に辺をこれ以上追加することはできないという意味から、極大という言葉が用いられています。 一方、最初の制約を破らない限り、色づけされていない頂点間の全ての辺は全て\(C\)に含める必要があります (ただし空集合は認められていません。) このような色分けは、\(C\)の辺数が可能な限り最小である場合にのみ、最小となります。

例題

例として、\(V=\{1, 2, 3, 4, 5\}\)と\(E=\{(1, 2), (1, 3), (2, 3), (3, 4), (4, 5)\}\)を持つようなグラフ\(G=(V, E)\)について考えましょう。 極大マッチング見つけるために、まずはマッチングとして空集合を用意します。 そして、2つの制約を破ることなく辺を追加することができなくなるまで、辺をその集合に追加していきます。 ここで考えているような小さなグラフでは、試行錯誤を繰り返すことで、人の手で最小極大マッチングを見つけることができるかもしれません。 この場合の答えは、\(\{(1, 2), (3, 4)\}\)または\(\{(1, 3), (4, 5)\}, \{(2, 3), (4, 5)\}\)となります。

数理モデル

辺\(e\)を色づけするかどうかを表すバイナリ変数を\(x_e\)を導入します。 これは、\(e\)が色付けされるとき1、そうでないとき0となるような変数です。 また、頂点\(v\)が\(C\)の辺に繋がれているとき1、そうでないとき0となるようなバイナリ変数\(y_v\)も導入します。

制約 1: \(x\)と\(y\)の関係式

これら2つのバイナリ変数の定義から、以下のような式を立てることができます。

\[ \quad y_v = \sum_{e \in E_v} x_e \quad \forall v, \]

ここで\(E_v\)は、頂点\(v\)につながる辺の集合です。

制約 2: 選ばれなかった全ての辺は、選ばれた辺につながる頂点のうち少なくとも1つにつながれてなければならない

これを定式化するために、\(1-y_u\)という量を用いましょう。 すると、これは\(u\)が選ばれた辺につながっている場合に0となります。 そして\((1-y_u)(1-y_v)\)を全ての辺\((u, v) \in E\)に対して数え上げれば、制約の破れをチェックすることができます (\((1-y_u)(1-y_v)\)>0ならば、辺\((u, v) \in E\)を制約の破れなく選択することができます。)

\[ \quad \sum_{(u,v)\in E} (1-y_u)(1-y_v) = 0. \]

目的関数: マッチングのサイズを最小化する

ここでのサイズとは、選択された辺の数を意味します。

\[ \quad \min \sum_{e \in E} x_e. \]

JijModelingによるモデル化

次に、JijModelingを用いて、上述の数式を実装しましょう。 最初に、数理モデルで用いられている変数を定義します。

import jijmodeling as jm

# define variables
V = jm.Placeholder('V')
E = jm.Placeholder('E', ndim=2)
num_E = E.shape[0]
x = jm.BinaryVar('x', shape=(num_E,))
y = jm.BinaryVar('y', shape=(V,))
v = jm.Element('v', V)
e = jm.Element('e', num_E)

制約と目的関数

制約と目的関数を実装しましょう。

problem = jm.Problem('Minimum Maximal Matching')
problem += jm.Constraint('y_x_relation', y[v] - jm.sum((e, (E[e][0]==v)|(E[e][1]==v)), x[e])  == 0 ,forall=v)
problem += jm.Constraint('unselected_edge', jm.sum(e, (1-y[E[e][0]])*(1-y[E[e][1]]))==0)

problem += x[:].sum()

Jupyter Notebook上で、実装した数式を表示してみましょう。

problem

\[\begin{split}\begin{array}{cccc}\text{Problem:} & \text{Minimum Maximal Matching} & & \\& & \min \quad \displaystyle \sum_{\ast_{0} = 0}^{\mathrm{len}\left(E, 0\right) - 1} x_{\ast_{0}} & \\\text{{s.t.}} & & & \\ & \text{unselected\_edge} & \displaystyle \sum_{e = 0}^{\mathrm{len}\left(E, 0\right) - 1} \left(- y_{E_{e, 0}} + 1\right) \cdot \left(- y_{E_{e, 1}} + 1\right) = 0 & \\ & \text{y\_x\_relation} & \displaystyle y_{v} - \sum_{\substack{e = 0\\E_{e, 0} = v \lor E_{e, 1} = v}}^{\mathrm{len}\left(E, 0\right) - 1} x_{e} = 0 & \forall v \in \left\{0,\ldots,V - 1\right\} \\\text{{where}} & & & \\& x & 1\text{-dim binary variable}\\& y & 1\text{-dim binary variable}\\\end{array}\end{split}\]

インスタンスの準備

ここでは、先ほど例題として示したグラフを用いましょう。

import networkx as nx

# set empty graph
inst_G = nx.Graph()
V = [0, 1, 2, 3, 4]
# add edges
inst_E = [[0, 1], [0, 2], [1, 2], [2, 3], [3, 4]] 
inst_G.add_edges_from(inst_E)
# get the number of nodes
inst_V = list(inst_G.nodes)
num_V = len(inst_V)
instance_data = {'V': num_V, 'E': inst_E}

このグラフを描画すると、次のようになります。

import matplotlib.pyplot as plt

pos = nx.spring_layout(inst_G)
nx.draw_networkx(inst_G, pos=pos, with_labels=True)
plt.show()

JijSolverで解く

jijsolverを用いて、この問題を解きましょう。

import jijsolver

interpreter = jm.Interpreter(instance_data)
instance = interpreter.eval_problem(problem)
solution = jijsolver.solve(instance, time_limit_sec=1.0)

解の可視化

得られた解を可視化してみましょう。

import numpy as np

# get the indices of x == 1
df = solution.decision_variables
x_indices = np.ravel(df[(df["name"] == "x") & (df["value"] == 1.0)]["subscripts"].to_list())
# get the indices of y == 1
y_indices = np.ravel(df[(df["name"] == "y") & (df["value"] == 1.0)]["subscripts"].to_list())
# set color list for visualization
cmap = plt.get_cmap("tab10")
# set vertex color
vertex_colors = [cmap(1) if i in y_indices else cmap(0) for i in inst_V]
# set edge color list
edge_colors = ["red" if j in x_indices else "black" for j, _ in enumerate(instance_data["E"])]
# dwaw the figure with two subplots
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))
# plot the initial graph
nx.draw_networkx(inst_G, pos, with_labels=True, ax=ax1)
ax1.set_title('Initial Graph')
plt.axis('off')
ax1.set_frame_on(False) # Remove the frame from the first subplot
# plot the minimum maximal matching graph
nx.draw_networkx(inst_G, pos=pos, node_color=vertex_colors, edge_color=edge_colors, with_labels=True)
plt.axis('off')
ax2.set_title('Minimum Maximal Matching Graph')
# Show the plot
plt.show()

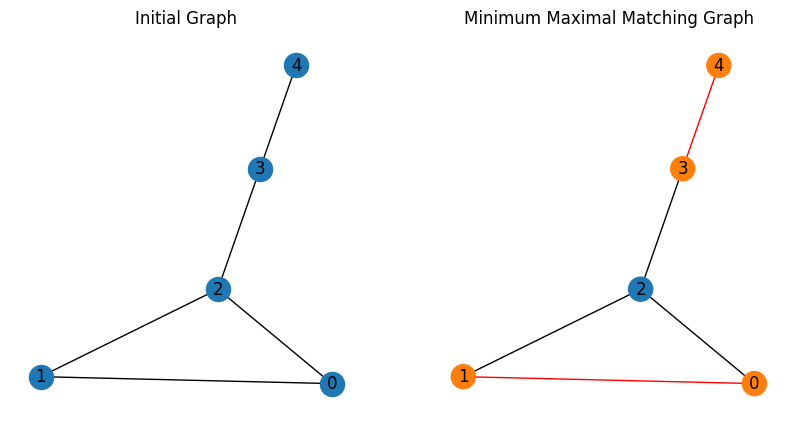
期待通り、最小極大マッチンググラフを得ることができました。